You are going to go through NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers. This post presents to the students a clear conception of how to move with the basics of Extra Questions and answers. The expert prepared The Extra Questions and And Answers. https://cbsencertanswers.com/is very much to make things way simpler and easier for the students. Especially those who are appearing for the board exams. We took every care to make sure that the effort serves the purpose. So, let us find out NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers. On this page, you can find NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers.

Exercise 1.1
1: Use Euclid’s division algorithm to find the HCF of:
i. 135 and 225a
ii. 196 and 38220
iii. 867 and 225
Solutions:
i. 135 and 225
As you can see, from the question 225 is greater than 135. Therefore, by Euclid’s division algorithm, we
have,
225 = 135 × 1 + 90
Now, remainder 90 ≠ 0, thus again using division lemma for 90, we get,
135 = 90 × 1 + 45
Again, 45 ≠ 0, repeating the above step for 45, we get, 90 = 45 × 2 + 0
The remainder is now zero, so our method stops here. Since, in the last step, the divisor is 45, therefore, HCF (225,135) = HCF (135, 90) = HCF (90, 45) = 45.
Hence, the HCF of 225 and 135 is 45.
ii. 196 and 38220
In this given question, 38220>196, therefore the by applying Euclid’s division algorithm and taking
38220 as divisor, we get, 38220 = 196 × 195 + 0
We have already got the remainder as 0 here. Therefore, HCF(196, 38220) = 196. Hence, the HCF of 196 and 38220 is 196.
iii. 867 and 225
As we know, 867 is greater than 225. Let us apply now Euclid’s division algorithm on 867, to get,
867 = 225 × 3 + 102
Remainder 102 ≠ 0, therefore taking 225 as divisor and applying the division lemma method, we get, 225 = 102 × 2 + 51
Again, 51 ≠ 0. Now 102 is the new divisor, so repeating the same step we get,
102 = 51 × 2 + 0
The remainder is now zero, so our procedure stops here. Since, in the last step, the divisor is 51, therefore, HCF (867,225) = HCF(225,102) = HCF(102,51) = 51.
Hence, the HCF of 867 and 225 is 51.
YOU ARE READING: NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers
2: Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is some integer.
Solution:
Let a be any positive integer and b = 6. Then, by Euclid’s algorithm, a = 6q + r, for some integer q ≥ 0, and r = 0, 1, 2, 3, 4, 5, because 0≤r<6.
Now substituting the value of r, we get, If r = 0, then a = 6q
Similarly, for r= 1, 2, 3, 4 and 5, the value of a is 6q+1, 6q+2, 6q+3, 6q+4 and 6q+5, respectively.
If a = 6q, 6q+2, 6q+4, then a is an even number and divisible by 2. A positive integer can be either even or odd Therefore, any positive odd integer is of the form of 6q+1, 6q+3 and 6q+5, where q is some integer.
YOU ARE READING: NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers
3. An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Solution:
Given,
Number of army contingent members=616 Number of army band members = 32
If the two groups have to march in the same column, we have to find out the highest common factor between the two groups. HCF(616, 32), gives the maximum number of columns in which they can march.
By Using Euclid’s algorithm to find their HCF, we get, Since, 616>32, therefore,
616 = 32 × 19 + 8
Since, 8 ≠ 0, therefore, taking 32 as new divisor, we have,
32 = 8 × 4 + 0
Now we have got remainder as 0, therefore, HCF (616, 32) = 8. Hence, the maximum number of columns in which they can march is 8.
4. Use Euclid’s division lemma to show that the square of any positive integer is either of theform 3m or 3m + 1 for some integer m.
Solutions:
Let x be any positive integer and y = 3.
By Euclid’s division algorithm, then,
x = 3q + r for some integer q≥0 and r = 0, 1, 2, as r ≥ 0 and r < 3.
Therefore, x = 3q, 3q+1 and 3q+2
Now as per the question given, by squaring both the sides, we get, x2 = (3q)2 = 9q2 = 3 × 3q2
Let 3q2 = m
Therefore, x2= 3m (1)
x2 = (3q + 1)2 = (3q)2+12+2×3q×1 = 9q2 + 1 +6q = 3(3q2+2q) +1
Substitute, 3q2+2q = m, to get,
x2= 3m + 1 (2)
x2= (3q + 2)2 = (3q)2+22+2×3q×2 = 9q2 + 4 + 12q = 3 (3q2 + 4q + 1)+1
Again, substitute, 3q2+4q+1 = m, to get, x2= 3m + 1… (3)
Hence, from equation 1, 2 and 3, we can say that, the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
YOU ARE READING: NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers
5. Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.
Solution:
Let x be any positive integer and y = 3.
By Euclid’s division algorithm, then,
x = 3q+r, where q≥0 and r = 0, 1, 2, as r ≥ 0 and r < 3.
Therefore, putting the value of r, we get,
x = 3q or
x = 3q + 1
or x = 3q + 2
Now, by taking the cube of all the three above expressions, we get,
Case (i): When r = 0, then,
x2= (3q)3 = 27q3= 9(3q3)= 9m; where m = 3q3
Case (ii): When r = 1, then,
x3 = (3q+1)3 = (3q)3 +13+3×3q×1(3q+1) = 27q3+1+27q2+9q
Taking 9 as common factor, we get, x3 = 9(3q3+3q2+q)+1
Putting (3𝑞3 + 3𝑞2 + 𝑞) = m, we get,
Putting (3q3+3q2+q) = m, we get , x3 = 9m+1
Case (iii): When r = 2, then,
x3 = (3q+2)3= (3q)3+23+3×3q×2(3q+2) = 27q3+54q2+36q+8
Taking 9 as common factor, we get, x3=9(3q3+6q2+4q)+8
Putting (3q3+6q2+4q) = m, we get , x3 = 9m+8
Therefore, from all the three cases explained above, it is proved that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.
YOU ARE READING: NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers
Exercise 1.2
1. Express each number as a product of its prime factors:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
Solutions:
(i) 140
By Taking the LCM of 140, we will get the product of its prime factor.
Therefore, 140 = 2 × 2 × 5 × 7 × 1 = 22×5×7
(ii) 156
By Taking the LCM of 156, we will get the product of its prime factor.
Hence, 156 = 2 × 2 × 13 × 3 × 1 = 22× 13 × 3
(iii) 3825
By Taking the LCM of 3825, we will get the product of its prime factor.
Hence, 3825 = 3 × 3 × 5 × 5 × 17 × 1 = 32×52×17
(iv) 5005
By Taking the LCM of 5005, we will get the product of its prime factor.
Hence, 5005 = 5 × 7 × 11 × 13 × 1 = 5 × 7 × 11 × 13
(v) 7429
By Taking the LCM of 7429, we will get the product of its prime factor.
Hence, 7429 = 17 × 19 × 23 × 1 = 17 × 19 × 23
YOU ARE READING: NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers
2. Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers.
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54
Solutions:
(i) 26 and 91
Expressing 26 and 91 as product of its prime factors, we get, 26 = 2 × 13 × 1
91 = 7 × 13 × 1
Therefore, LCM (26, 91) = 2 × 7 × 13 × 1 = 182
And HCF (26, 91) = 13
Verification
Now, product of 26 and 91 = 26 × 91 = 2366
And Product of LCM and HCF = 182 × 13 = 2366 Hence, LCM × HCF = product of the 26 and 91.
(ii) 510 and 92
Expressing 510 and 92 as product of its prime factors, we get, 510 = 2 × 3 × 17 × 5 × 1
92 = 2 × 2 × 23 × 1
Therefore, LCM(510, 92) = 2 × 2 × 3 × 5 × 17 × 23 = 23460
And HCF (510, 92) = 2
Verification
Now, product of 510 and 92 = 510 × 92 = 46920 And Product of LCM and HCF = 23460 × 2 = 46920 Hence, LCM × HCF = product of the 510 and 92.
(iii) 336 and 54
Expressing 336 and 54 as product of its prime factors, we get, 336 = 2 × 2 × 2 × 2 × 7 × 3 × 1
54 = 2 × 3 × 3 × 3 × 1
Therefore, LCM(336, 54) = 24 × 33 × 7 = 3024
And HCF(336, 54) = 2×3 = 6
Verification
Now, product of 336 and 54 = 336 × 54 = 18,144 And Product of LCM and HCF = 3024 × 6 = 18,144 Hence, LCM × HCF = product of the 336 and 54.
YOU ARE READING: NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers
3. Find the LCM and HCF of the following integers by applying the prime factorization method.
(i) 12, 15 and 21
(ii) 17, 23 and 29
(iii) 8, 9 and 25
Solutions:
(i) 12, 15 and 21
Writing the product of prime factors for all the three numbers, we get, 12=2×2×3
15=5×3
21=7×3
Therefore, HCF(12,15,21) = 3
LCM(12,15,21) = 2 × 2 × 3 × 5 × 7 = 420
(ii) 17, 23 and 29
Writing the product of prime factors for all the three numbers, we get, 17=17×1
23=23×1
29=29×1
Therefore,
HCF(17,23,29) = 1
LCM(17,23,29) = 17 × 23 × 29 = 11339
(iii) 8, 9 and 25
Writing the product of prime factors for all the three numbers, we get, 8=2×2×2×1
9=3×3×1
25=5×5×1
Therefore, HCF(8,9,25)=1
LCM(8,9,25) = 2×2×2×3×3×5×5 = 1800
4. Given that HCF (306, 657) = 9, find LCM (306, 657).
Solutions:
As we know that,
HCF×LCM=Product of the two given numbers Therefore,
9 × LCM = 306 × 657
LCM = (306×657)/9 = 22338 Hence, LCM(306,657) = 22338
YOU ARE READING: NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers
5. Check whether 6n can end with the digit 0 for any natural number n.
Solutions:
If the number 6n ends with the digit zero (0), then it should be divisible by 5, as we know any number with unit place as 0 or 5 is divisible by 5.
Prime factorization of 6n = (2×3)n
Therefore, the prime factorization of 6n doesn’t contain the prime number 5.
Hence, it is clear that for any natural number n, 6n is not divisible by 5 and thus it proves that 6n cannot end with the digit 0 for any natural number n.
6. Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
Solutions:
By the definition of a composite number, we know, if a number is composite, then it means it has factors other than 1 and itself. Therefore, for the given expression;
7 × 11 × 13 + 13
Taking 13 as a common factor, we get,
=13(7×11×1+1) = 13(77+1) = 13×78 = 13×3×2×13
Hence, 7 × 11 × 13 + 13 is a composite number.
Now let’s take the other number,
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
Taking 5 as a common factor, we get,
=5(7×6×4×3×2×1+1) = 5(1008+1) = 5×1009
Hence, 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 is a composite number.
7. There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
Solutions:
Since, Both Sonia and Ravi move in the same direction and at the same time, the method to find the time when they will be meeting again at the starting point is LCM of 18 and 12.
Therefore, LCM(18,12) = 2×3×3×2×1=36
Hence, Sonia and Ravi will meet again at the starting point after 36 minutes.
Exercise 1.3
1.Prove that √5 is irrational.
Solutions:
Let us assume, that √5 is rational number.
i.e. √5 = x/y (where, x and y are co-primes) y√5= x
Squaring both the sides, we get, (y√5)2 = x2
⇒5y2 = x2(1)
Thus, x2 is divisible by 5, so x is also divisible by 5.
Let us say, x = 5k, for some value of k and substituting the value of x in equation (1), we get, 5y2 = (5k)2
⇒y2 = 5k2
𝒚𝟐 is divisible by 5 it means y is divisible by 5.
Therefore, x and y are co-primes. Since, our assumption about √5 is rational is incorrect. Hence, √5 is irrational number.
YOU ARE READING: NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers
2. Prove that 3 + 2√5 + is irrational.
Solutions:
Let us assume 3 + 2√5 is rational.
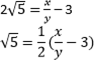
Then we can find co-prime x and y (y ≠ 0) such that 3 + 2√5 = x/y Rearranging, we get,
Since, x and y are integers, thus,
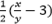
is a rational number
Therefore, √5 is also a rational number. But this contradicts the fact that √5 is irrational. So, we conclude that 3 + 2√5 is irrational.
3. Prove that the following are irrationals:
(i) 1/√2
(ii) 7√5
(iii) 6 + √2
Solutions:
(i) 1/√2
Let us assume 1/√2 is rational.
Then we can find co-prime x and y (y ≠ 0) such that 1/√2 = x/y Rearranging, we get,
√2 = y/x
Since x and y are integers, thus, √2 is a rational number, which contradicts the fact that √2 is irrational. Hence, we can conclude that 1/√2 is irrational.
YOU ARE READING: NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers
(ii) 7√5
Let us assume 7√5 is a rational number.
Then we can find co-prime a and b (b ≠ 0) such that 7√5 = x/y Rearranging, we get,
√5 = x/7y
Since x and y are integers, thus, √5 is a rational number, which contradicts the fact that √5 is irrational. Hence, we can conclude that 7√5 is irrational.
(iii) 6 +√2
Let us assume 6 +√2 is a rational number.
Then we can find co-primes x and y (y ≠ 0) such that 6 +√2 = x/y⋅ Rearranging, we get,
√2 = (x/y) – 6
Since x and y are integers, thus (x/y) – 6 is a rational number and therefore, √2 is rational. This contradicts the fact that √2 is an irrational number.
Hence, we can conclude that 6 +√2 is irrational.
YOU ARE READING: NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers
Exercise 1.4
1. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
(i) 13/3125 (ii) 17/8 (iii) 64/455 (iv) 15/1600 (v) 29/343 (vi) 23/(2352) (vii) 129/(225775) (viii) 6/15 (ix) 35/50 (x) 77/210
Solutions:
Note: If the denominator has only factors of 2 and 5 or in the form of 2m ×5n then it has a terminating decimal expansion.
If the denominator has factors other than 2 and 5 then it has a non-terminating decimal expansion.
(i) 13/3125
Factorizing the denominator, we get, 3125 = 5 × 5 × 5 = 55
Since, the denominator has only 5 as its factor, 13/3125 has a terminating decimal expansion.
(ii) 17/8
Factorizing the denominator, we get,
8 = 2×2×2 = 23
Since, the denominator has only 2 as its factor, 17/8 has a terminating decimal expansion.
(iii) 64/455
Factorizing the denominator, we get,
455 = 5×7×13
Since, the denominator is not in the form of 2m × 5n, thus 64/455 has a non-terminating decimal expansion.
YOU ARE READING: NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers
(iv) 15/ 1600
Factorizing the denominator, we get,
1600 = 2652
Since, the denominator is in the form of 2m × 5n, thus 15/1600 has a terminating decimal expansion.
(v) 29/343
Factorizing the denominator, we get,
343 = 7×7×7 = 73 Since, the denominator is not in the form of 2m × 5n thus 29/343 has a non-terminating decimal expansion.
(vi) 23/(2352)
Clearly, the denominator is in the form of 2m × 5n. Hence, 23/ (2352) has a terminating decimal expansion.
(vii) 129/(225775)
As you can see, the denominator is not in the form of 2m × 5n. Hence, 129/ (225775) has a non-terminating decimal expansion.
(viii) 6/15
6/15 = 2/5
Since the denominator has only 5 as its factor, thus, 6/15 has a terminating decimal expansion.
(ix) 35/50
35/50 = 7/10
Factorising the denominator, we get, 10 = 2 × 5
Since the denominator is in the form of 2m × 5n thus, 35/50 has a terminating decimal expansion.
(x) 77/210
77/210 = (7× 11)/ (30 × 7) = 11/30
Factorizing the denominator, we get, 30 = 2 × 3 × 5
As you can see, the denominator is not in the form of 2m × 5n . Hence, 77/210 has a non-terminating decimal expansion.
YOU ARE READING: NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers
2. Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.
Solutions:
(i) 13/3125

13/3125 = 0.00416
YOU ARE READING: NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers
(ii) 17/8

17/8 = 2.125
(iii) 64/455 has a Non-terminating decimal expansion
YOU ARE READING: NCERT Solutions For Class 10 CBSE Mathematics Chapter 1 Real Numbers
(iv)15/ 1600

15/1600 = 0.009375
(v) 29/ 343 has a Non terminating decimal expansion
(vi) 23/ (2352) = 23/(8×25)= 23/200
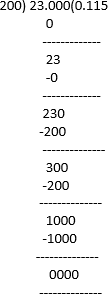
23/ (2352) = 0.115
(vii) 129/ (225775) has a Non terminating decimal expansion
(viii) 6/15 = 2/5
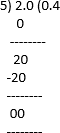
6/15 = 0.4
(ix) 35/50 = 7/10

35/50 = 0.7
(x) 77/210 has a non-terminating decimal expansion.
3. The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form, p q what can you say about the prime factors of q?
(i) 43.123456789
(ii) 0.120120012000120000. . .
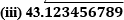
Solutions:
(i) 43.123456789
Since it has a terminating decimal expansion, it is a rational number in the form of p/q and q has factors of 2 and 5 only.
(ii) 0.120120012000120000. . .
Since it has a non-terminating and non-repeating decimal expansion, it is an irrational number.
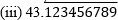
Since it has a non-terminating but repeating decimal expansion, it is a rational number in the form of p/q and q has factors other than 2 and 5.