You are going to go through Some Applications of Trigonometry Chapter 9 Extra Questions and Solutions For Class 10 CBSE Mathematics. This post presents to the students a clear conception of how to move with the basics of Extra Questions and answers. The expert prepared The Extra Questions and And Answers. https://cbsencertanswers.com/is very much to make things way simpler and easier for the students. Especially those who are appearing for the board exams. We took every care to make sure that the effort serves the purpose. So, let us find out Some Applications of Trigonometry Chapter 9 Extra Questions and Solutions For Class 10 CBSE Mathematics. On this page, you can find Some Applications of Trigonometry Chapter 9 Extra Questions and Solutions For Class 10 CBSE Mathematics.

1) A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2 m away from the wall and the ladder is making an angle of 60° with the level of the ground. Determine the height of the wall?
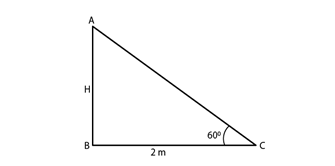
Solution.
Given,
Distance between the wall and the foot of the ladder = 2m = BC. Angle made by ladder with ground (θ) = 60°. Height of the wall (H) = AB.
Now, the fig. of ABC forms a right angle triangle.
So,
tan θ = (Opposite Side / Adjacent Side) = tan 60 = AB/BC = √3 = AB/2 = AB = 2 √3 m.
So, the height ( AB = H) of the wall is 2 √3 m.
2) The angle of elevation of a ladder against a wall is 60° and the foot of the ladder is 9.5 m away from the wall. Find the length of the ladder?
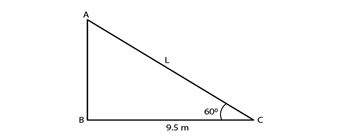
Solution.
Distance between the wall and foot of the ladder = 9.5 m. Angle of elevation (θ) = 60°. Length of the ladder = L = AC.
Now, from fig. ABC , ΔABC is a right angle triangle , So,

YOU ARE READING: Some Applications of Trigonometry Chapter 9 Extra Questions and Solutions For Class 10 CBSE Mathematics
Therefore, the length of the ladder AC is 19 m.
3) A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 60° to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable?
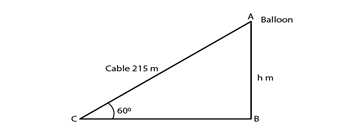
Solution.
Let the height of the balloon from the ground = h m.
It is given that , the length of the cable = 215 m and the inclination of the cable is 60o.
In right-angled triangle ΔABC,
sin 60o = AB/ AC
√3 / 2 = h / 215
h = 215 (√3/2) = 185.9
Therefore, the height of the balloon from the ground is 186m.
4) A ladder 15 metres long reaches the top of a vertical wall. If the ladder makes an angle of 60o with the wall, find the height of the wall?
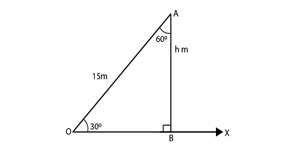
Solution.
It is given that ,
The length of the ladder = 15m = AO. Angle made by the ladder with the wall = 60o. Let the height of the wall be h metres and the horizontal ground taken as OX.
Then from the fig. we have,
In right ΔABO, using trigonometric ratios,
cos (60o) = AB/AO
1/2 = h/ 15
h = 15/2
h = 7.5m
YOU ARE READING: Some Applications of Trigonometry Chapter 9 Extra Questions and Solutions For Class 10 CBSE Mathematics
Hence, the height of the wall is 7.5m.
5) A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
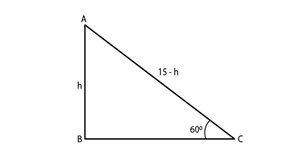
Solution.
Given,
The initial height of tree H = 15 m = AB + AC. We assume that it is broken at point A. And, the angle made by broken part with the ground (θ) = 60°. Height from ground to broken points = h = AB.
So, we have
H = AC + h
⟹ AC = (H – h) m = ( 15 – h ) m .
We get a right triangle formed by the above given data, So,
sin∅=oppositeside/hypotenuse
Now,
Sin60 = AB/ BC
√3/2=h/(H-h)
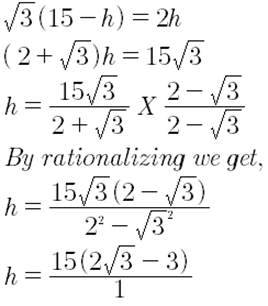
Therefore, the height of broken point from the ground is 15(2√3 – 3)m.
6) A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height 5 meters. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are respectively 30° and 60°. Find the height of the tower?
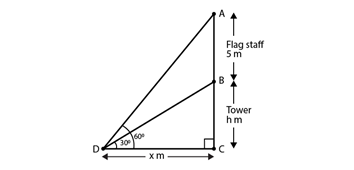
Solution.
Given,
Height of the flag staff = 5 m = AB, Angle of elevation of the top of flag staff = 60°
Angle of elevation of the bottom of the flagstaff = 30°. Let height of tower be ‘h’ m = BC . And, let the distance of the point from the base of the tower = x m.
In right angle triangle BCD, we have
tan 30o = BC/DC
1/√3 = h/x
x = h√3 ….. (i)
Now, in ΔACD,
tan 60o = AC/DC
√3 = (5 + h)/ x
√3x = 5 + h
√3(h√3) = 5 + h [using (i)]
3h = 5 + h
2h = 5
h = 5/2 = 2.5m
YOU ARE READING: Some Applications of Trigonometry Chapter 9 Extra Questions and Solutions For Class 10 CBSE Mathematics
Therefore, the height of the tower = 2.5 m.
7) A parachute is descending vertically and makes angles of elevation of 45° and 60° at two observing points 100 m apart from each other on the left side of himself. Find the maximum height from which he falls and the distance of point where he falls on the ground from the just observation point?
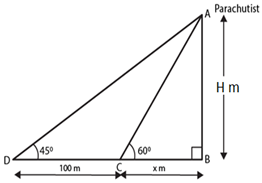
Solution.
Let the parachute at highest point A and let C and D be points which are 100 m apart on ground where from then CD = 100 m. Angle of elevation from point D = 45° = α . Angle of elevation from point C = 60° = β .
Let B be the point just vertically down the parachute.Now let us draw figure according to above data then it forms the figure as shown in which ABC and ABD are two triangles,
Maximum height of the parachute from the ground AB = H m . Distance of point where parachute falls to just nearest observation point = x m . If in right angle triangle one of the included angles is θ then …
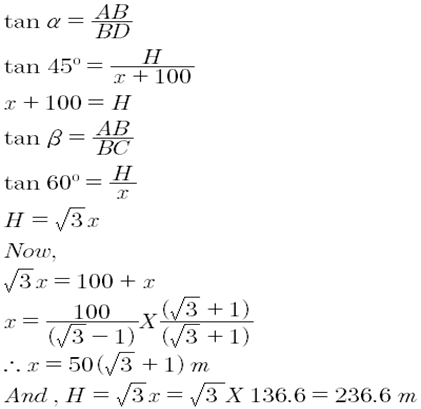
Therefore, The maximum height of the parachute from the ground, H = 236.6m. Distance between the two points where parachute falls on the ground and just the observation is x = 136.6 m.
8) The angle of elevation of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 meters towards the foot of the tower, the angle of elevation of the tower becomes 60°. Prove that the height of the tower is 129.9 metres?
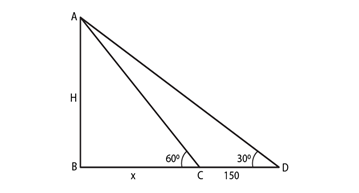
Solution.
Given,
The angle of elevation of top tower from first point D, α = 30°. On moving through D to C by 150 m, then CD = 150 m and angle of elevation of top of the tower from second point C, β = 60°. Let height of tower AB = H m.

YOU ARE READING: Some Applications of Trigonometry Chapter 9 Extra Questions and Solutions For Class 10 CBSE Mathematics
Therefore, it has been proved that the height of the tower is 129.9 m.
9) On a horizontal plane there is a vertical tower with a flag pole on the top of the tower. At a point 9 m away from the foot of the tower the angle of elevation of the top and bottom of the flag pole are 60° and 30° respectively. Find the height of the tower and the flag pole mounted on it?
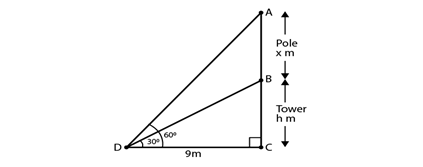
Solution.
Let BC be the tower and AB be the flag pole on the tower. Distance of the point of observation from foot of the tower DC = 9 m. Angle of elevation of top of flag pole is 60° and angle of elevation of bottom of flag pole is 30°.
Let height of the tower = h m = BC . and the height of the pole = x m = AB .
From fig, we have
In ΔBCD,
tan 30o = BC/DC
1/√3 = h/9
h = 9/√3 = 3√3
Next, in ΔACD
tan 60o = AC/DC
√3 = (x + h)/9
x + h = 9√3
x + 3√3 = 9√3
x = 6√3 m
Therefore, Height of the tower = 3√3 m and height of the pole = 6√3 m.
10) From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag staff from P is 45°. Find the length of the flag staff and the distance of the building from the point P?
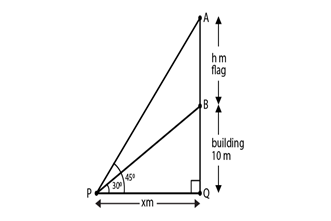
Solution.
Let the height of flag-staff(AB) = h m.
And, the distance PQ = x m.
Given,
Angle of elevation of top of the building = 30o.
Angle of elevation of top of the flag staff = 45o
From the fig.
In ΔBQP,
tan 30o = BQ/PQ
1/√3 = 10/x
x = 10√3 m
Next,
In ΔAQP,
tan 45o = AQ/PQ
1 = (h + 10)/x
h + 10 = x = 10√3
h = (10√3 – 10) = 10(1.732) – 10 = 17.32 – 10
= 7.32 m
YOU ARE READING: Some Applications of Trigonometry Chapter 9 Extra Questions and Solutions For Class 10 CBSE Mathematics
Therefore, the distance of point P from building = x = 10√3 = 10(1.732) = 17.32m
11) The shadow of a tower standing on level ground is found to be 40 m longer when Sun’s altitude is 30° than when it was 60°. Find the height of the tower?
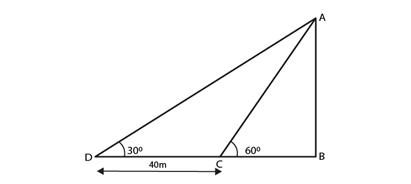
Solution.
When the sun’s altitude is the angle of elevation of the top of the tower from the tip of the shadow. . Let AB be h m and BC be x m. From the question, DC is 40 m longer than BC.
So, BD = (40 + x) m.
And two right triangles ABC and ABD are formed.
.
In ΔABC,
tan 60o = AB/ BC
√3 = h/x
x = h/√3 … (i)
In ΔABD,
tan 30o = AB/ BD
1/ √3 = h/ (x + 40)
x + 40 = √3h
h/√3 + 40 = √3h [using (i)]
h + 40√3 = 3h
2h = 40√3
h = 20√3
Therefore, the height of the tower is 20√3 m.
12) A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 10 meters. Find the height of the tree?
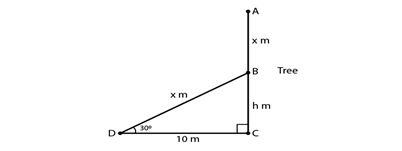
Solution.
Let AC be the height of the tree which is (x + h) m. Given, the broken portion of the tree is making an angle of 30o with the ground.
From the fig.
In ΔBCD, we have
tan 30o = BC/ DC
1/√3 = h/ 10
h = 10/ √3
Next, in ΔBCD
cos 30o = DC/BD
√3/2 = 10/x
x = 20/√3 m
So,
x + h = 20/√3 + 10/√3
= 30/√3
= 10√3 = 10(1.732) = 17.32
YOU ARE READING: Some Applications of Trigonometry Chapter 9 Extra Questions and Solutions For Class 10 CBSE Mathematics
Therefore, the height of the tree is 17.32 m.
13) The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m longer than when it was 60°. Find the height of the tower?
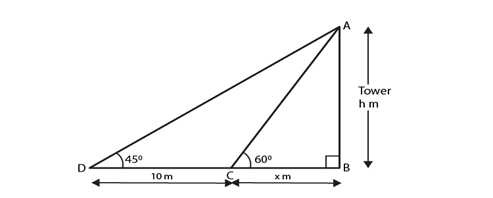
Solution.
Let the height of the tower(AB) = h m. Let the length of the shorter shadow be x m. Then, the longer shadow is (10 + x)m.
So, from fig. In ΔABC
tan 60o = AB/BC
√3 = h/x
x = h/√3…. (i)
Next, in ΔABD
tan 45o = AB/BD
1 = h/(10 + x)
10 + x = h
10 + (h/√3) = h [using (i)]
10√3 + h = √3h
h(√3 -1) =10√3
h = 10√3/ (√3 -1)
After rationalising the denominator, we have
h = [10√3 x (√3 + 1)]/ (3 – 1)
h = 5√3(√3 + 1)
h = 5(3 + √3) = 23.66 [√3 = 1.732]
Therefore, the height of the tower is 23.66 m.
14) On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects?
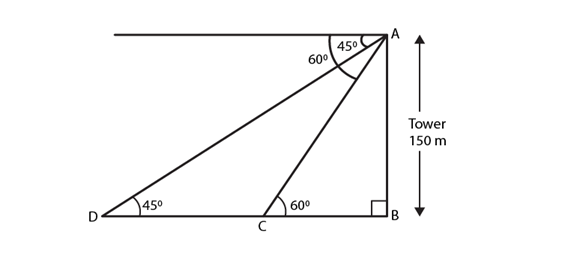
Solution.
Given,
The height of the tower (AB) = 150m. Angles of depressions of the two objects are 45o and 60o.
In ΔABD
tan 45o = AB/ BD
1 = 150/ BD
BD = 150m
Next, in ΔABC
tan 60o = AB/ BC
√3 = 150/ BC
BC = 150/√3
BC = 50√3 = 50(1.732) = 86.6 m
So,
DC = BD – BC = 150 – 86.6 = = 63.4
YOU ARE READING: Some Applications of Trigonometry Chapter 9 Extra Questions and Solutions For Class 10 CBSE Mathematics
Therefore, the distance between two objects = 63.4 m.
15) The angle of elevation of the top of a tower as observed from a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626]
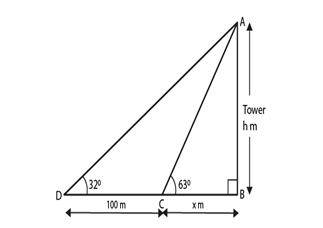
Solution.
Let the height of the tower = h m and the distance BC = x m.
Then, from the fig.
In ΔABC
tan 63o = AB/BC
1.9626 = h/x
x = h/ 1.9626
x = 0.5095 h …. (i)
Next, in ΔABD
tan 32o = AB/ BD
0.6248 = h/ (100 + x)
h = 0.6248(100 + x)
h = 62.48 + 0.6248x
h = 62.48 + 0.6248(0.5095 h) ….. [using (i)]
h = 62.48 + 0.3183h
0.6817h = 62.48
h = 62.48/0.6817 = 91.65
Using h in (i), we have
x = 0.5095(91.65) = 46.69
Therefore,
The height of the tower is 91.65 m and distance of the first position from the tower = 100 + x = 146.69 m.
16) A 1.6 m tall girl stands at a distance of 3.2 m from a lamp post and casts a shadow of 4.8 m on the ground. Find the height of the lamp post by using (i) trigonometric ratio (ii) properties of similar triangles.
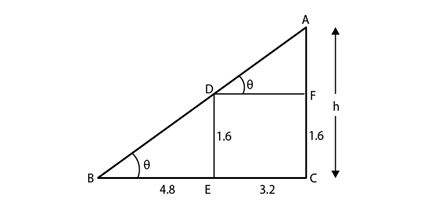
Solution.
Let AC be the lamp post of height ‘h’ and DE is the tall girl and her shadow is BE. So, we have ED = 1.6 m, BE = 4.8 m and EC = 3.2
(i) By using trigonometric ratio
In ΔBDE,
tan θ = 1.6/4.8
tan θ = 1/3
Next, In ΔABC
tan θ = h/ (4.8 + 3.2)
1/3 = h/8
h = 8/3 m
ii) By using similar triangles
Since triangle BDE and triangle ABC are similar (by AA criteria), we have
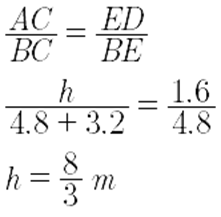
YOU ARE READING: Some Applications of Trigonometry Chapter 9 Extra Questions and Solutions For Class 10 CBSE Mathematics
Therefore, the height of the lamp post is h = 8/3 m.
17) A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal?
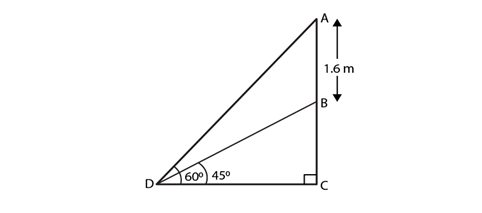
Solution.
Let’s assume AB as the statue, BC be the pedestal and D be the point on ground from where elevation angles are measured. It is given that the Angle of elevation of the top of statue is 60o and angle of elevation of the top of the pedestal is 45o.
So, from the fig. we have
In ΔBCD,
tan 45o = BC/ CD
1 = BC/ CD
CD = BC
Next, In ΔADC
tan 60o = (AB + BC)/ CD
√3 = (AB + BC)/ BC [As CD = BC, found above]
BC√3 = AB + BC
AB = (√3 – 1)BC
BC = AB/ (√3 – 1)
BC = 1.6/ (√3 – 1)
Rationalising the denominator, we have
BC = 1.6(√3 + 1)/ 2
BC = 0.8(√3 + 1) m
Therefore, the height of pedestal is 0.8(√3 + 1) m
18) From the top of a 7 m high building, the angle of elevation of the top of a cable is 60° and the angel of depression of its foot is 45°. Determine the height of the tower?
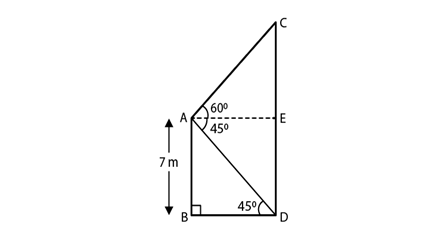
Solution.
Given
Height of the building = 7 m = AB and height of the cable tower = CD.
Angle of elevation of the top of the cable tower from the top of the building = 60° and angle of depression of the bottom of the building from the top of the building= 45°.
Then, from the fig. we see that
ED = AB = 7 m
And,
CD = CE + ED
So, In ΔABD, we have
AB/ BD = tan 45o
AB = BD = 7
BD = 7
In ΔACE,
AE = BD = 7
And, tan 60o = CE/AE
√3 = CE/ 7
CE = 7√3 m
So, CD = CE + ED = (7√3 + 7)= 7(√3 + 1) m
YOU ARE READING: Some Applications of Trigonometry Chapter 9 Extra Questions and Solutions For Class 10 CBSE Mathematics
Therefore, the height of the cable tower is 7(√3 + 1)m.
19) The angle of elevation of the top of the building from the foot of the tower is 30° and the angle of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building?
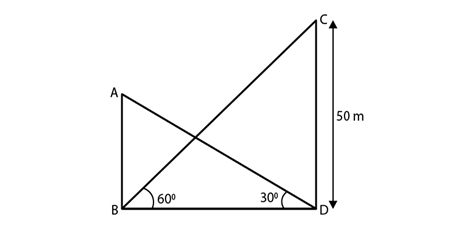
Solution.
Let AB be the building and CD be the tower. It is given that The angle of elevation of the top of the building from the foot of the tower is 30o and the angle of elevation of the top of the building from the foot of the tower is 30o.
Height of the tower = CD = 50 m
From the fig. we have
In ΔCDB,
CD/ BD = tan 60o
50/ BD = √3
BD = 50/√3 …. (i)
Next in ΔABD,
AB/ BD = tan 30o
AB/ BD = 1/√3
AB = BD/ √3
AB = 50/√3/ (√3) [From (i)]
AB = 50/3
Therefore, the height of the building is 50/3 m.
20 ) The length of the shadow of a tower standing on level plane is found to be 2x meters longer when the sun’s attitude is 30° than when it was 30°. Prove that the height of tower is x(√3+1) meters?
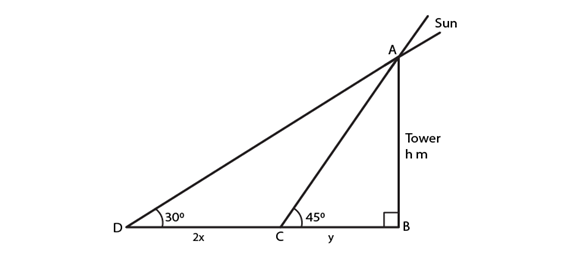
Solution.
From the question, the following fig. is made , Let the height of tower (AB) = h m and distance BC = y m.
Then, in ΔABC
tan 45o = AB/BC
1 = h/y
y = h
Next, in ΔABD
tan 30o = AB/BD
1/√3 = h/ (2x + y)
2x + y = √3h
2x + h = √3h
2x = (√3 – 1)h
h = 2x/ (√3 – 1) x (√3 + 1)/ (√3 + 1)
h = 2x (√3 + 1)/(3-1) = 2x (√3 + 1)/2 = x (√3 + 1)
Therefore, the height of the tower is x (√3 + 1) m
Hence Proved the height.
YOU ARE READING: Some Applications of Trigonometry Chapter 9 Extra Questions and Solutions For Class 10 CBSE Mathematics
.