You are going to go through Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics. This post presents to the students a clear conception of how to move with the basics of Extra Questions and answers. The expert prepared The Extra Questions and And Answers. https://cbsencertanswers.com/is very much to make things way simpler and easier for the students. Especially those who are appearing for the board exams. We took every care to make sure that the effort serves the purpose. So, let us find out Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics. On this page, you can find Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics.

Ex 5.1
1. In which of the following situations, does the list of numbers involved make as arithmetic progression and why? (i) The taxi fare after each km when the fare is Rs 15 for the first km and Rs 8 for each additional km.
Solution:
We can write the given condition as;
Taxi fare for 1 km = 15
Taxi fare for first 2 kms = 15+8 = 23
Taxi fare for first 3 kms = 23+8 = 31
Taxi fare for first 4 kms = 31+8 = 39
And so on……
Thus, 15, 23, 31, 39 … forms an A.P.
because every next term is 8 more than the preceding term.
(ii) The amount of air present in a cylinder when a vacuum pump removes 1/4 of the air remaining in the cylinder at a time.
Solution:
Let the volume of air in a cylinder, initially, be V litres.
In each stroke, the vacuum pump removes 1/4th of air remaining in the cylinder at a time.
Or we can say, after every stroke, 1-1/4 = 3/4th part of air will remain.
Therefore, volumes will be V, 3V/4 , (3V/4)2 , (3V/4)3 …and so on
Clearly, we can see here, the adjacent terms of this series do not have the common difference between them. Therefore, this series is not an A.P.
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
(iii) The cost of digging a well after every metre of digging, when it costs Rs 150 for the first metre and rises by Rs 50 for each subsequent metre.
Solution:
We can write the given condition as;
Cost of digging a well for first metre = Rs.150
Cost of digging a well for first 2 metres = Rs.150+50 = Rs.200
Cost of digging a well for first 3 metres = Rs.200+50 = Rs.250
Cost of digging a well for first 4 metres =Rs.250+50 = Rs.300
And so on..
Clearly, 150, 200, 250, 300 … forms an A.P. with a common difference of 50 between each term.
(iv) The amount of money in the account every year, when Rs 10000 is deposited at compound interest at 8% per annum.
Solution:
We know that if Rs. P is deposited at r% compound interest per annum for n years,
the amount of money will be: P(1+r/100)n
Therefore, after each year, the amount of money will be;
10000(1+8/100), 10000^(1+8/100)2, 10000^(1+8/100)3……
Clearly, the terms of this series do not have the common difference between them.
Therefore, this is not an A.P.
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
2. Write first four terms of the A.P. when the first term a and the common difference are given as follows:
(i) a = 10, d = 10
(ii) a = -2, d = 0
(iii) a = 4, d = – 3
(iv) a = -1 d = ½
(v) a = – 1.25, d = – 0.25
Solutions:
(i) a = 10, d = 10
Let us consider, the Arithmetic Progression series be a1, a2, a3, a4, a5 …
a1 = a = 10
a2 = a1+d = 10+10 = 20
a3 = a2+d = 20+10 = 30
a4 = a3+d = 30+10 = 40
a5 = a4+d = 40+10 = 50
And so on…
Therefore, the A.P. series will be 10, 20, 30, 40, 50 … And First four terms of this A.P. will be 10, 20, 30, and 40.
(ii) a = – 2, d = 0
Let us consider, the Arithmetic Progression series be a1, a2, a3, a4, a5 …
a1 = a = -2
a2 = a1+d = – 2+0 = – 2
a3 = a2+d = – 2+0 = – 2
a4 = a3+d = – 2+0 = – 2
Therefore, the A.P. series will be – 2, – 2, – 2, – 2 …
And, First four terms of this A.P. will be – 2, – 2, – 2 and – 2.
(iii) a = 4, d = – 3
Let us consider, the Arithmetic Progression series be a1, a2, a3, a4, a5 …
a1 = a = 4
a2 = a1+d = 4-3 = 1
a3 = a2+d = 1-3 = – 2
a4 = a3+d = -2-3 = – 5
Therefore, the A.P. series will be 4, 1, – 2 – 5 …
And, first four terms of this A.P. will be 4, 1, – 2 and – 5.
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
(iv) a = – 1, d = ½
Let us consider, the Arithmetic Progression series be a1, a2, a3, a4, a5 …
a2 = a1+d = -1+1/2 = -½
a3 = a2+d = -1/2+1/2 = 0
a4 = a3+d = 0+1/2 = ½
Thus, the A.P. series will be-1, -1/2, 0, 1/2
And First four terms of this A.P. will be -1, -1/2, 0 and 1/2.
(v) a = – 1.25, d = – 0.25
Let us consider, the Arithmetic Progression series be a1, a2, a3, a4, a5 …
a1 = a = – 1.25
a2 = a1 + d = – 1.25-0.25 = – 1.50
a3 = a2 + d = – 1.50-0.25 = – 1.75
a4 = a3 + d = – 1.75-0.25 = – 2.00
Therefore, the A.P series will be 1.25, – 1.50, – 1.75, – 2.00 ……..
And first four terms of this A.P. will be – 1.25, – 1.50, – 1.75 and – 2.00.
3. For the following A.P.s, write the first term and the common difference.
(i) 3, 1, – 1, – 3 …
(ii) -5, – 1, 3, 7 …
(iii) 1/3, 5/3, 9/3, 13/3 ….
(iv) 0.6, 1.7, 2.8, 3.9 …
Solutions
(i) Given series, 3, 1, – 1, – 3 …
First term, a = 3
Common difference, d = Second term – First term
⇒ 1 – 3 = -2
⇒ d = -2
(ii) Given series, – 5, – 1, 3, 7 …
First term, a = -5
Common difference, d = Second term – First term
⇒ ( – 1)-( – 5) = – 1+5 = 4
(iii) Given series, 1/3, 5/3, 9/3, 13/3 ….
First term, a = 1/3
Common difference, d = Second term – First term
⇒ 5/3 – 1/3 = 4/3
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
(iv) Given series, 0.6, 1.7, 2.8, 3.9 …
First term, a = 0.6
Common difference, d = Second term – First term
⇒ 1.7 – 0.6 ⇒ 1.1
4. Which of the following are APs? If they form an A.P. find the common difference d and write three more terms. (i) 2, 4, 8, 16 …
(ii) 2, 5/2, 3, 7/2 ….
(iii) -1.2, -3.2, -5.2, -7.2 …
(iv) -10, – 6, – 2, 2 …
(v) 3, 3 + √2, 3 + 2√2, 3 + 3√2
(vi) 0.2, 0.22, 0.222, 0.2222 ….
(vii) 0, – 4, – 8, – 12 …
(viii) -1/2, -1/2, -1/2, -1/2 ….
(ix) 1, 3, 9, 27 …
(x) a, 2a, 3a, 4a …
(xi) a, a 2 , a 3 , a 4 …
(xii) √2, √8, √18, √32 …
(xiii) √3, √6, √9, √12 …
(xiv) 1, 9, 25, 49 …..
(xv) 1, 25, 49, 73 …
Solution
(i) Given to us,2, 4, 8, 16 …
Here, the common difference is;
a2 – a1 = 4 – 2 = 2
a3 – a2 = 8 – 4 = 4
a4 – a3 = 16 – 8 = 8
Since, an+1 – an or the common difference is not the same every time.
Therefore, the given series are not forming an A.P.
(ii) Given, 2, 5/2, 3, 7/2 ….
Here, a2 – a1 = 5/2-2 = ½
a3 – a2 = 3-5/2 = 1/2
a4 – a3 = 7/2-3 = 1/2
Since, an+1 – an or the common difference is same every time.
Therefore, d = 1/2 and the given series are in A.P.
The next three terms are;
a5 = 7/2+1/2 = 4
a6 = 4 +1/2 = 9/2
a7 = 9/2 +1/2 = 5
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
(iii) Given, -1.2, – 3.2, -5.2, -7.2 …
Here, a2 – a1 = (-3.2)-(-1.2) = -2
a3 – a2 = (-5.2)-(-3.2) = -2
a4 – a3 = (-7.2)-(-5.2) = -2
Since, an+1 – an or common difference is same every time.
Therefore, d = -2 and the given series are in A.P.
Hence, next three terms are;
a5 = – 7.2-2 = -9.2
a6 = – 9.2-2 = – 11.2
a7 = – 11.2-2 = – 13.2
(iv) Given, -10, – 6, – 2, 2 …
Here, the terms and their difference are;
a2 – a1 = (-6)-(-10) = 4
a3 – a2 = (-2)-(-6) = 4
a4 – a3 = (2 -(-2) = 4
Since, an+1 – an or the common difference is same every time.
Therefore, d = 4 and the given numbers are in A.P.
Hence, next three terms are;
a5 = 2+4 = 6
a6 = 6+4 = 10
a7 = 10+4 = 14
(v) Given, 3, 3+√2, 3+2√2, 3+3√2
Here, a2 – a1 = 3+√2-3 = √2
a3 – a2 = (3+2√2)-(3+√2) = √2
a4 – a3 = (3+3√2) – (3+2√2) = √2
Since, an+1 – an or the common difference is same every time.
Therefore, d = √2 and the given series forms a A.P.
Hence, next three terms are;
a5 = (3+√2) +√2 = 3+4√2
a6 = (3+4√2)+√2 = 3+5√2
a7 = (3+5√2)+√2 = 3+6√2
(vi) 0.2, 0.22, 0.222, 0.2222 ….
Here, a2 – a1 = 0.22-0.2 = 0.02
a3 – a2 = 0.222-0.22 = 0.002
a4 – a3 = 0.2222-0.222 = 0.0002
Since, an+1 – an or the common difference is not same every time.
Therefore, and the given series doesn’t forms a A.P.
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
(vii) 0, -4, -8, -12 …
Here, a2 – a1 = (-4)-0 = -4
a3 – a2 = (-8)-(-4) = -4
a4 – a3 = (-12)-(-8) = -4
Since, an+1 – an or the common difference is same every time.
Therefore, d = -4 and the given series forms a A.P.
Hence, next three terms are; a5 = -12-4 = -16
a6 = -16-4 = -20
a7 = -20-4 = -24
(viii) -1/2, -1/2, -1/2, -1/2 ….
Here, a2 – a1 = (-1/2) – (-1/2) = 0
a3 – a2 = (-1/2) – (-1/2) = 0
a4 – a3 = (-1/2) – (-1/2) = 0
Since, an+1 – an or the common difference is same every time.
Therefore, d = 0 and the given series forms a A.P
. Hence, next three terms are;
a5 = (-1/2)-0 = -1/2
a6 = (-1/2)-0 = -½
a7 = (-1/2)-0 = -½
(ix) 1, 3, 9, 27 …
Here, a2 – a1 = 3-1 = 2
a3 – a2 = 9-3 = 6
a4 – a3 = 27-9 = 18
Since, an+1 – an or the common difference is not same every time.
Therefore, and the given series doesn’t form a A.P.
(x) a, 2a, 3a, 4a …
Here, a2 – a1 = 2a-a = a
a3 – a2 = 3a-2a = a
a4 – a3 = 4a-3a = a
Since, an+1 – an or the common difference is same every time.
Therefore, d = a and the given series forms a A.P.
Hence, next three terms are;
a5 = 4a+a = 5a
a6 = 5a+a = 6a
a7 = 6a+a = 7a
(xi) a, a2, a3, a4…
Here, a2 – a1 = a2 -a = a(a-1)
a3 – a2 = a3 – a2 = a2(a-1)
a4 – a3 = a4 – a3 = a3 (a-1)
Since, an+1 – an or the common difference is not same every time.
Therefore, the given series doesn’t form a A.P.
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
(xii) √2, √8, √18, √32 …
Here, a2 – a1 = √8-√2 = 2√2-√2 = √2
a3 – a2 = √18-√8 = 3√2-2√2 = √2
a4 – a3 = 4√2-3√2 = √2
Since, an+1 – an or the common difference is same every time.
Therefore, d = √2 and the given series forms a A.P.
Hence, next three terms are;
a5 = √32+√2 = 4√2+√2 = 5√2 = √50
a6 = 5√2+√2 = 6√2 = √72
a7 = 6√2+√2 = 7√2 = √98
(xiii) √3, √6, √9, √12 …
Here, a2 – a1 = √6-√3 = √3×√2-√3 = √3(√2-1)
a3 – a2 = √9-√6 = 3-√6 = √3(√3-√2)
a4 – a3 = √12 – √9 = 2√3 – √3×√3 = √3(2-√3)
Since, an+1 – an or the common difference is not same every time.
Therefore, the given series doesn’t form a A.P.
(xiv) 1, 9, 25, 49 …..
Here, a2 − a1 = 9−1 = 8
a3 − a2 = 25−9 = 16
a4 − a3 = 49−25 = 24
Since, an+1 – an or the common difference is not same every time.
Therefore, the given series doesn’t form a A.P.
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
(xv) 1, 25, 49, 73 …
Here, a2 − a1 = 25−1 = 24
a3 − a2 = 49−25 = 24
a4 − a3 = 73−49 = 24
Since, an+1 – an or the common difference is same every time.
Therefore, d = 24 and the given series forms a A.P.
Hence, next three terms are;
a5 = 73+24 = 97
a6 = 97+24 = 121
a7 = 121+24 = 145.
Ex 5.2
1. Fill in the blanks in the following table, given that a is the first term, d the common difference and an the nth term of the A.P.
| a | d | n | an | |
| (I) | 7 | 3 | 8 | ……….. |
| (ii) | -18 | ……… | 10 | 0 |
| (iii) | …………. | -3 | 18 | -5 |
| (iv) | -18.9 | 2.5 | ………… | 3.6 |
| (v) | 3.5 | 0 | 105 | ……….. |
Solutions:
(i) Given, First term, a = 7
Common difference, d = 3
Number of terms, n = 8,
We have to find the nth term, an = ?
As we know, for an A.P., an = a+(n−1)d
Putting the values,
=> 7+(8 −1) 3 = 7+(7) 3 = 7+21 = 28
Hence, an = 28
(ii) Given, First term, a = -18
Common difference, d = ?
Number of terms, n = 10
Nth term, an = 0
As we know, for an A.P., an = a+(n−1)d
Putting the values,
0 = − 18 +(10−1)d
18 = 9d
d = 18/9 = 2
Hence, common difference, d = 2
(iii) Given, First term, a = ?
Common difference, d = -3
Number of terms, n = 18
Nth term, an = -5
As we know, for an A.P.,
an = a+(n−1)d
Putting the values, −5 = a+(18−1) (−3)
−5 = a+(17) (−3)
−5 = a−51
a = 51−5 = 46
Hence, a = 46
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
(iv) Given, First term, a = -18.9
Common difference, d = 2.5
Number of terms, n = ?
Nth term, an = 3.6
As we know, for an A.P.,
an = a +(n −1)d
Putting the values, 3.6 = − 18.9+(n −1)2.5
3.6 + 18.9 = (n−1)2.5
22.5 = (n−1)2.5 (n – 1) = 22.5/2.5
n – 1 = 9
n = 10
Hence, n = 10
(v) Given, First term, a = 3.5
Common difference, d = 0
Number of terms, n = 105
Nth term, an = ?
As we know, for an A.P., an = a+(n −1)d
Putting the values, an = 3.5+(105−1) 0
an = 3.5+104×0
an = 3.5
Hence, an = 3.5 2.
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
Choose the correct choice in the following and justify:
(i) 30th term of the A.P: 10,7, 4, …, is
(A) 97 (B) 77 (C) −77 (D) −87
(ii) 11th term of the A.P. -3, -1/2, ,2 …. is
(A) 28 (B) 22 (C) – 38 (D)
Solutions:
(i) Given here, A.P. = 10, 7, 4, …
Therefore, we can find,
First term, a = 10
Common difference, d = a2 − a1 = 7−10 = −3
As we know, for an A.P., an = a +(n−1)d
Putting the values; a30 = 10+(30−1)(−3)
a30 = 10+(29)(−3)
a30 = 10−87 = −77
Hence, the correct answer is option C.
(ii) Given here, A.P. = -3, -1/2, ,2 …
Therefore, we can find, First term a = – 3
Common difference, d = a2 − a1 = (-1/2) -(-3) =(-1/2) + 3 = 5/2
As we know, for an A.P., an = a+(n−1)d
Putting the values; a11 = 3+(11-1)(5/2)
a11 = 3+(10)(5/2)
a11 = -3+25
a11 = 22
Hence, the answer is option B.
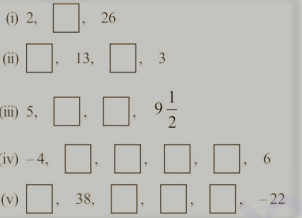
3. In the following APs find the missing term in the boxes.
Solutions:
(i) For the given A.P., 2,….. , 26
The first and third term are; a = 2
a3 = 26
As we know, for an A.P., an = a+(n −1)d
Therefore, putting the values here, a3 = 2+(3-1)d
26 = 2+2d
24 = 2d
d = 12
a2 = 2+(2-1)12 = 14.
Therefore, 14 is the missing term.
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
(ii) For the given A.P…….., 13,……… ,3
a2 = 13 and a4 = 3
As we know, for an A.P., an = a+(n−1) d
Therefore, putting the values here, a2 = a +(2-1)d
13 = a+d ………………. (i)
a4 = a+(4-1)d
3 = a+3d ………….. (ii)
On subtracting equation (i) from (ii), we get,
– 10 = 2d
d = – 5
From equation (i), putting the value of d,we get
13 = a+(-5)
a = 18
a3 = 18+(3-1)(-5) = 18+2(-5) = 18-10 = 8
Therefore, the missing terms are 18 and 8 respectively.
(iii) For the given A.P., a = 5 and a4 = 19/2
As we know, for an A.P., an = a+(n−1)d
Therefore, putting the values here, a4 = a+(4-1)d 19/2 = 5+3d (19/2) – 5 = 3d
3d = 9/2
d = 3/2
a2 = a+(2-1)d
a2 = 5+3/2
a2 = 13/2
a3 = a+(3-1)d
a3 = 5+2×3/2
a3 = 8
Therefore, the missing terms are 13/2 and 8 respectively.
(iv) For the given A.P., a = −4 and a6 = 6
As we know, for an A.P., an = a +(n−1) d
Therefore, putting the values here,
a6 = a+(6−1)d
6 = − 4+5d
10 = 5d
d = 2
a2 = a+d = − 4+2 = −2
a3 = a+2d = − 4+2(2) = 0
a4 = a+3d = − 4+ 3(2) = 2
a5 = a+4d = − 4+4(2) = 4
Therefore, the missing terms are −2, 0, 2, and 4 respectively.
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
(v) For the given A.P., a2 = 38 a6 = −22
As we know, for an A.P., an = a+(n −1)d
Therefore, putting the values here,
a2 = a+(2−1)d
38 = a+d ……………………. (i)
a6 = a+(6−1)d
−22 = a+5d …………………. (ii)
On subtracting equation (i) from (ii), we get
− 22 − 38 = 4d −60 = 4d
d = −15
a = a2 − d = 38 − (−15) = 53
a3 = a + 2d = 53 + 2 (−15) = 23
a4 = a + 3d = 53 + 3 (−15) = 8
a5 = a + 4d = 53 + 4 (−15) = −7
Therefore, the missing terms are 53, 23, 8, and −7 respectively.
4. Which term of the A.P. 3, 8, 13, 18, … is 78?
Solutions:
Given the A.P. series as3, 8, 13, 18, …
First term, a = 3 Common difference, d = a2 − a1 = 8 − 3 = 5
Let the n th term of given A.P. be 78.
Now as we know, an = a+(n−1)d
Therefore, 78 = 3+(n −1)5
75 = (n−1)5 (n−1) = 15
n = 16
Hence, 16th term of this A.P. is 78.
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
5. Find the number of terms in each of the following A.P. (i) 7, 13, 19, …, 205
Solutions:
(i) Given, 7, 13, 19, …, 205 is the A.P
Therefore First term, a = 7
Common difference, d = a2 − a1 = 13 − 7 = 6
Let there are n terms in this A.P. an = 205
As we know, for an A.P., an = a + (n − 1) d
Therefore, 205 = 7 + (n − 1) 6
198 = (n − 1) 6
33 = (n − 1)
n = 34
Therefore, this given series has 34 terms in it.
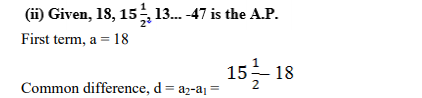
d = (31-36)/2 = -5/2
Let there are n terms in this A.P. an = 205
As we know, for an A.P., an = a+(n−1)d
-47 = 18+(n-1)(-5/2)
-47-18 = (n-1)(-5/2)
-65 = (n-1)(-5/2)
(n-1) = -130/-5
(n-1) = 26
n = 27
Therefore, this given A.P. has 27 terms in it.
6. Check whether -150 is a term of the A.P. 11, 8, 5, 2, …
Solution:
For the given series, A.P. 11, 8, 5, 2..
First term, a = 11
Common difference, d = a2−a1 = 8−11 = −3
Let −150 be the n th term of this A.P.
As we know, for an A.P., an = a+(n−1)d
-150 = 11+(n -1)(-3)
-150 = 11-3n +3
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
-164 = -3n
n = 164/3
Clearly, n is not an integer but a fraction.
Therefore, – 150 is not a term of this A.P.
7. Find the 31st term of an A.P. whose 11th term is 38 and the 16th term is 73.
Solution:
Given that, 11th term, a11 = 38 and 16th term, a16 = 73
We know that, an = a+(n−1)d
a11 = a+(11−1)d
38 = a+10d ………………………………. (i)
In the same way, a16 = a +(16−1)d
73 = a+15d ………………………………………… (ii)
On subtracting equation (i) from (ii), we get
35 = 5d
d = 7
From equation (i), we can write,
38 = a+10×(7)
38 − 70 = a
a = −32
a31 = a +(31−1) d = − 32 + 30 (7) = − 32 + 210 = 178
Hence, 31st term is 178.
8. An A.P. consists of 50 terms of which 3rd term is 12 and the last term is 106.Find the 29th term.
Solution:
Given that, 3 rd term, a3 = 12
50th term, a50 = 106
We know that, an = a+(n−1)d
a3 = a+(3−1)d 12 = a+2d ……………………………. (i)
In the same way, a50 = a+(50−1)d
106 = a+49d …………………………. (ii)
On subtracting equation (i) from (ii), we get
94 = 47d
d = 2 = common difference
From equation (i), we can write now,
12 = a+2(2)
a = 12−4 = 8
a29 = a+(29−1) d
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
a29 = 8+(28)2
a29 = 8+56 = 64
Therefore, 29th term is 64.
9. If the 3rd and the 9th terms of an A.P. are 4 and − 8 respectively. Which term of this A.P. is zero.
Solution:
Given that, 3 rd term, a3 = 4 and 9th term, a9 = −8
We know that, an = a+(n−1)d
Therefore, a3 = a+(3−1)d
4 = a+2d ……………………………………… (i)
a9 = a+(9−1)d
−8 = a+8d ………………………………………………… (ii)
On subtracting equation (i) from (ii), we will get here,
−12 = 6d
d = −2
From equation (i), we can write,
4 = a+2(−2) 4 = a−4
a = 8
Let n th term of this A.P. be zero.
an = a+(n−1)d
0 = 8+(n−1)(−2)
0 = 8−2n+2
2n = 10
n = 5
Hence, 5th term of this A.P. is 0.
10. If 17th term of an A.P. exceeds its 10th term by 7. Find the common difference.
Solution:
We know that, for an A.P series;
an = a+(n−1)d
a17 = a+(17−1)d
a17 = a +16d
In the same way,
a10 = a+9d
As it is given in the question,
a17 − a10 = 7
Therefore, (a +16d)−(a+9d) = 7
7d = 7
d = 1
Therefore, the common difference is 1.
11. Which term of the A.P. 3, 15, 27, 39,.. will be 132 more than its 54th term?
Solution:
Given A.P. is 3, 15, 27, 39, …
first term, a = 3 common difference, d = a2 − a1 = 15 − 3 = 12
We know that, an = a+(n−1)d
Therefore, a54 = a+(54−1)d
⇒3+(53)(12)
⇒3+636 = 639
a54 = 639
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
We have to find the term of this A.P. which is 132 more than a54, i.e.771.
Let n th term be 771. an = a+(n−1)d
771 = 3+(n −1)12
768 = (n−1)12
(n −1) = 64
n = 65
Therefore, 65th term was 132 more than 54th term.
12. Two APs have the same common difference. The difference between their 100th term is 100, what is the difference between their 1000th terms?
Solution:
Let, the first term of two APs be a1 and a2 respectively
And the common difference of these APs be d.
For the first A.P.,we know,
an = a+(n−1)d
Therefore, a100 = a1+(100−1)d = a1 + 99d
a1000 = a1+(1000−1)d
a1000 = a1+999d
For second A.P., we know,
an = a+(n−1)d
Therefore,
a100 = a2+(100−1)d = a2+99d
a1000 = a2+(1000−1)d = a2+999d
Given that, difference between 100th term of the two APs = 100
Therefore, (a1+99d) − (a2+99d) = 100
a1−a2 = 100……………………………………………………………….. (i)
Difference between 1000th terms of the two APs (a1+999d) − (a2+999d) = a1−a2
From equation (i),
This difference, a1−a2 = 100
Hence, the difference between 1000th terms of the two A.P. will be 100.
13. How many three digit numbers are divisible by 7?
Solution:
First three-digit number that is divisible by 7 are;
First number = 105
Second number = 105+7 = 112
Third number = 112+7 =119
Therefore, 105, 112, 119, …
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
All are three digit numbers are divisible by 7 and thus, all these are terms of an A.P. having first term as 105 and common difference as 7.
As we know, the largest possible three-digit number is 999.
When we divide 999 by 7, the remainder will be 5.
Therefore, 999-5 = 994 is the maximum possible three-digit number that is divisible by 7.
Now the series is as follows. 105, 112, 119, …, 994
Let 994 be the nth term of this A.P. first term, a = 105 common difference, d = 7
an = 994 n = ?
As we know, an = a+(n−1)d
994 = 105+(n−1)7
889 = (n−1)7 (n−1) = 127
n = 128
Therefore, 128 three-digit numbers are divisible by 7.
14. How many multiples of 4 lie between 10 and 250?
Solution:
The first multiple of 4 that is greater than 10 is 12. Next multiple will be 16. Therefore, the series formed as;
12, 16, 20, 24, …
All these are divisible by 4 and thus, all these are terms of an A.P. with first term as 12 and common difference as 4.
When we divide 250 by 4, the remainder will be 2.
Therefore, 250 − 2 = 248 is divisible by 4.
The series is as follows, now; 12, 16, 20, 24, …, 248
Let 248 be the n th term of this A.P. first term, a = 12 common difference, d = 4
an = 248
As we know, an = a+(n−1)d
248 = 12+(n-1)×4
236/4 = n-1
59 = n-1
n = 60
Therefore, there are 60 multiples of 4 between 10 and 250.
15. For what value of n, are the n th terms of two APs 63, 65, 67, and 3, 10, 17, … equal?
Solution:
Given two APs as; 63, 65, 67,… and 3, 10, 17,….
Taking first AP, 63, 65, 67, …
First term, a = 63 Common difference, d = a2−a1 = 65−63 = 2
We know, n th term of this A.P. = an = a+(n−1)d
an= 63+(n−1)2 = 63+2n−2
an = 61+2n ………………………………………. (i)
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
Taking second AP, 3, 10, 17, …
First term, a = 3 Common difference, d = a2 − a1 = 10 − 3 = 7
We know that, n th term of this A.P. = 3+(n−1)7
an = 3+7n−7
an = 7n−4 ……………………………………………………….. (ii)
Given, n th term of these A.P.s are equal to each other.
Equating both these equations, we get,
61+2n = 7n−4
61+4 = 5n
5n = 65
n = 13
Therefore, 13th terms of both these A.P.s are equal to each other.
16. Determine the A.P. whose third term is 16 and the 7th term exceeds the 5th term by 12.
Solutions:
Given, Third term, a3 = 16
As we know, a +(3−1)d = 16
a+2d = 16 ………………………………………. (i)
It is given that, 7 th term exceeds the 5th term by 12.
a7 − a5 = 12 [a+(7−1)d]−[a +(5−1)d]= 12
(a+6d)−(a+4d) = 12
2d = 12
d = 6
From equation (i), we get,
a+2(6) = 16
a+12 = 16
a = 4
Therefore, A.P. will be4, 10, 16, 22, …
17. Find the 20th term from the last term of the A.P. 3, 8, 13, …, 253.
Solution:
Given A.P. is3, 8, 13, …, 253 Common difference, d= 5.
Therefore, we can write the given AP in reverse order as; 253, 248, 243, …, 13, 8, 5
Now for the new AP, first term, a = 253
and common difference, d = 248 − 253 = −5
n = 20 Therefore, using nth term formula, we get,
a20 = a+(20−1)d
a20 = 253+(19)(−5)
a20 = 253−95
a = 158
Therefore, 20th term from the last term of the AP 3, 8, 13, …, 253.is 158.
18. The sum of 4th and 8th terms of an A.P. is 24 and the sum of the 6th and 10th terms is 44. Find the first three terms of the A.P.
Solution:
We know that, the nth term of the AP is;
an = a+(n−1)d
a4 = a+(4−1)d
a4 = a+3d
YOU ARE READING: Arithmetic Progressions Chapter 5 NCERT Solutions For Class 10 CBSE Mathematics
In the same way, we can write,
a8 = a+7d
a6 = a+5d
a10 = a+9d
Given that,
a4+a8 = 24 a+3d+a+7d = 24
2a+10d = 24
a+5d = 12 …………………………………………………… (i)
a6+a10 = 44
a +5d+a+9d = 44
2a+14d = 44
a+7d = 22 …………………………………….. (ii)
On subtracting equation (i) from (ii), we get,
2d = 22 − 12
2d = 10
d = 5
From equation (i), we get,
a+5d = 12
a+5(5) = 12
a+25 = 12
a = −13
a2 = a+d = − 13+5 = −8
a3 = a2+d = − 8+5 = −3
Therefore, the first three terms of this A.P. are −13, −8, and −3.
19. Subba Rao started work in 1995 at an annual salary of Rs 5000 and received an increment of Rs 200 each year. In which year did his income reach Rs 7000?
Solution:
It can be seen from the given question, that the incomes of Subba Rao increases every year by Rs.200 and hence, forms an AP.
Therefore, after 1995, the salaries of each year are; 5000, 5200, 5400, …
Here, first term, a = 5000 and common difference, d = 200
Let after n th year, his salary be Rs 7000.
Therefore, by the n th term formula of AP,
an = a+(n−1) d
7000 = 5000+(n−1)200
200(n−1)= 2000
(n−1) = 10
n = 11
Therefore, in 11th year, his salary will be Rs 7000.
20. Ramkali saved Rs 5 in the first week of a year and then increased her weekly saving by Rs 1.75. If in the n th week, her weekly savings become Rs 20.75, find n.
Solution:
Given that, Ramkali saved Rs.5 in first week and then started saving each week by Rs.1.75.
Hence, First term, a = 5 and common difference, d = 1.75
Also given, an = 20.75 Find, n = ?
As we know, by the nth term formula,
an = a+(n−1)d
Therefore, 20.75 = 5+(n -1)×1.75
15.75 = (n -1)×1.75
(n -1) = 15.75/1.75 = 1575/175 = 63/7 = 9
n -1 = 9
n = 10 Hence, n is 10.