You are going to go through Circles Chapter 10 Extra Questions and Solutions For Class 10 CBSE Mathematics. This post presents to the students a clear conception of how to move with the basics of Extra Questions and answers. The expert prepared The Extra Questions and And Answers. https://cbsencertanswers.com/is very much to make things way simpler and easier for the students. Especially those who are appearing for the board exams. We took every care to make sure that the effort serves the purpose. So, let us find out Circles Chapter 10 Extra Questions and Solutions For Class 10 CBSE Mathematics. On this page, you can find Circles Chapter 10 Extra Questions and Solutions For Class 10 CBSE Mathematics.

1)A point P is at a distance of 29 cm from the centre of a circle of radius 20 cm. Find the length of the tangent drawn from P to the circle?
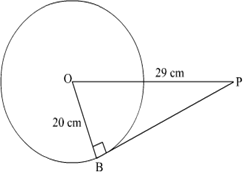
Solution.
Considering the figure, We know that the tangent is perpendicular to the radius of a circle.
So, OPB is a right angled triangle, with ∠OBP=90°
By using pythagoras theorem in △OPB, we get
⇒ OB2+PB2=OP2
⇒ (20)2+PB2=(29)2
⇒ 400+PB2=841
⇒ PB2=841-400=441⇒PB=√441=21
So, length of the tangent from point P is 21 cm(PB) .
2) A point P is 25 cm away from the centre of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle?
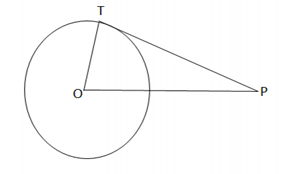
Solution.
A point P is 25 cm away from the centre of a circle and the length of tangent drawn from P to the circle is 24 cm.So, TP here is the tangent , OT is the radius So, OTP is a right angled triangle, with ∠OTP=90°
By using pythagoras theorem in △OTP, we get
⇒ OT2+TP2=OP2
⇒ (OT)2+(24)2=(25)2
⇒ OT2+576=625
⇒ OT2=625 – 576=49⇒OT=√49=7 cm.
YOU ARE READING: Circles Chapter 10 Extra Questions and Solutions For Class 10 CBSE Mathematics
Hence, the radius OT is 7 cm.
3) Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle?
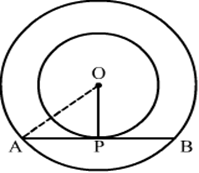
Solution.
In this given figure, we know that the radius and tangent are perperpendular at their point of contact
In right triangle △AOP,
AO2 = OP2 + PA2
⇒ (6.5)2 = (2.5)2 + PA2
⇒ PA2 = 36
⇒ PA = 6 cm
Since, the perpendicular drawn from the centre bisect the chord.
∴ PA = PB = 6 cm
Now, AB = AP + PB = 6 + 6 = 12 cm
Hence, the length of the chord of the larger circle (AB) is 12 cm.
4) In the given figure, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB
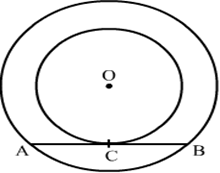
Solution.
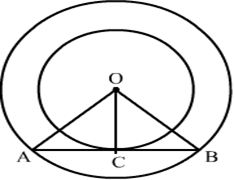
Construction: Join OA, OC and OB
We know that the radius and tangent are perpendicular at their point of contact
∴ ∠OCA = ∠OCB = 90∘
Now, In △OCA and △OCB
∠OCA = ∠OCB = 90∘
OA = OB (Radii of the larger circle)
OC = OC (Common)
△OCA ≅ △OCB (By RHS congruency
∴ CA = CB ( Proved).
YOU ARE READING: Circles Chapter 10 Extra Questions and Solutions For Class 10 CBSE Mathematics
5) In the given figure, an isosceles triangle ABC with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC ?
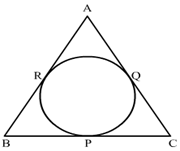
Solution.
We know that, tangent segments to a circle from the same external point are congruent.
Now, we have
AR = AQ, BR = BP and CP = CQ
Now, AB = AC as △ ABC is isosceles triangle
⇒ AR + RB = AQ + QC
⇒ AR + RB = AR + QC
⇒ RB = QC
⇒ BP = CP
Hence, P bisects BC at P.
6) In the given figure, a circle with centre O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29 cm, AD = 23 cm, ∠B = 90∘ and DS = 5 cm then find the radius of the circle?
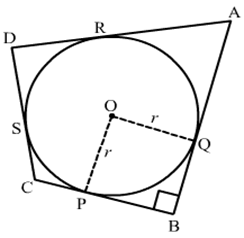
Solution.
We know that tangent segments to a circle from the same external point are congruent.
Now, we have
DS = DR, AR = AQ
Now, AD = 23 cm
⇒ AR + RD = 23
⇒ AR = 23 − RD
⇒ AR = 23 − 5 [∵ DS = DR = 5]
⇒ AR = 18 cm
Again, AB = 29 cm
⇒ AQ + QB = 29
⇒ QB = 29 − AQ
⇒ QB = 29 − 18 [∵ AR = AQ = 18]
⇒ QB = 11 cm
Since all the angles are in a quadrilateral BQOP are right angles and OP = BQ.
Hence, BQOP is a square.
We know that all the sides of square are equal.
Therefore, BQ = PO = 11 cm
Hence, the radius of the circle is 11 cm.
YOU ARE READING: Circles Chapter 10 Extra Questions and Solutions For Class 10 CBSE Mathematics
7) In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of AD?
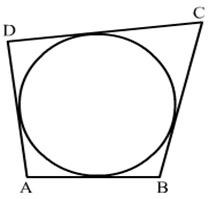
Solution.
We know that when a quadrilateral circumscribes a circle then sum of opposites sides is equal to the sum of other opposite sides.
∴ AB + CD = AD + BC
⇒6 + 8 = AD + 9
⇒ AD = 5 cm
Hence, the length of AD is 5 cm.
8) In the given figure, O is the centre of a circle PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70∘ then ∠TRQ ?
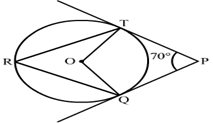
Solution.
We know that the radius and tangent are perperpendular at their point of contact
∵∠OTP = ∠OQP = 90∘
Now, In quadrilateral OQPT
∠QOT + ∠OTP + ∠OQP + ∠TPQ = 360∘ [Angle sum property of a quadrilateral]
⇒ ∠QOT + 90∘ + 90∘ + 70∘ = 360∘
⇒ 250∘ + ∠QOT = 360∘
⇒ ∠QOT = 110∘
We know that the angle subtended by an arc at the centre is double the angle subtended by the arc at any point on the remaining part of the circle.
∴ , ∠TRQ = ½ (∠QOT) = 55∘ .
9) In the given figure, AB and AC are tangents to a circle with centre O such that ∠BAC = 40∘ .Then find the value of ∠BOC?
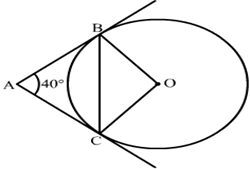
Solution.
We know that the radius and tangent are perperpendular at their point of contact
∵∠OBA = ∠OCA = 90∘
Now, In quadrilateral ABOC
∠BAC + ∠OCA + ∠OBA + ∠BOC = 360∘ [Angle sum property of a quadrilateral]
⇒ 40∘ + 90∘ + 90∘ + ∠BOC = 360∘
⇒ 220∘ + ∠BOC = 360∘
⇒ ∠BOC = 140∘
Then the value of ∠BOC is 140∘ .
YOU ARE READING: Circles Chapter 10 Extra Questions and Solutions For Class 10 CBSE Mathematics
10) In the given figure, ∠AOD = 135∘ then find the angle ∠BOC ?
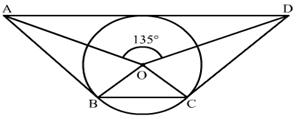
Solution.
We know that the sum of angles subtended by opposite sides of a quadrilateral having a circumscribed circle is 180 degrees.
∴∠AOD + ∠BOC = 180∘
⇒∠BOC = 180∘ − 135∘ = 45∘
11) In the given figure, O is the centre of the circle. AB is the tangent to the circle at the point P. If ∠PAO = 30∘ then find the value of the sum of angles ∠CPB + ∠ACP ?
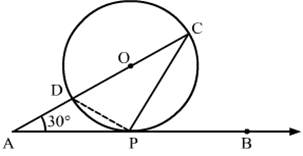
Solution.
We know that a chord passing through the centre is the diameter of the circle.
∵∠DPC = 90∘ (Angle in a semi circle is 90∘)
Now, In △CDP
∠CDP + ∠DCP + ∠DPC = 180∘ [Angle sum property of a triangle]
⇒ ∠CDP + ∠DCP + 90∘ = 180∘
⇒ ∠CDP + ∠DCP = 90∘
By using alternate segment theorem
We have ∠CDP = ∠CPB
∴∠CPB + ∠ACP = 90∘
12) In the given figure, two circles touch each other at C and AB is a tangent to both the circles. Then find the value of ∠ACB ?
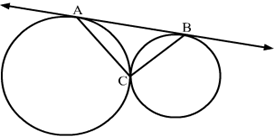
Solution.
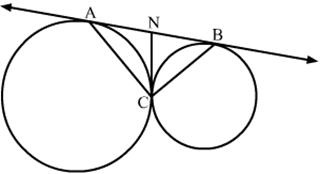
We know that tangent segments to a circle from the same external point are congruent.
Therefore, we have NA = NC and NC = NB. We also know that angle opposite to equal sides are equal.
∴ ∠NAC = ∠NCA and ∠NBC = ∠NCB
Now, ∠ANC + ∠BNC = 180∘ [Linear pair angles]
⇒ ∠NBC + ∠NCB + ∠NAC + ∠NCA= 180∘ [Exterior angle property]
⇒ 2∠NCB + 2∠NCA= 180∘
⇒ 2(∠NCB + ∠NCA) = 180∘
⇒ ∠ACB = 90∘
YOU ARE READING: Circles Chapter 10 Extra Questions and Solutions For Class 10 CBSE Mathematics
13) In the given figure, O is the centre of a circle, BOA is its diameter and the tangent at the point P meets BA extended at T. If ∠PBO = 30∘ then the value of ∠PTA ?
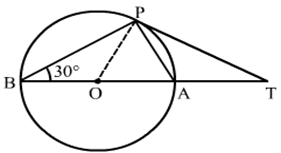
Solution.
We know that a chord passing through the centre is the diameter of the circle.
∵∠BPA = 90∘ (Angle in a semi circle is 90∘)
By using alternate segment theorem
We have ∠APT = ∠ABP = 30∘
Now, In △ABP
∠PBA + ∠BPA + ∠BAP = 1800 [Angle sum property of a triangle]
⇒ 30∘ + 900 + ∠BAP = 180∘
⇒ ∠BAP = 60∘
Now, ∠BAP = ∠APT + ∠PTA
⇒ 60∘ = 30∘ + ∠PTA
⇒ ∠PTA = 30∘
14) In the given figure, a circle touches the side DF of △EDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm then the perimeter of △EDF is ?
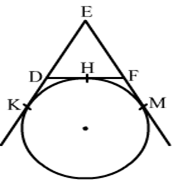
Solution.
We know that tangent segments to a circle from the same external point are congruent.
Therefore, we have
EK = EM = 9 cm
Now, EK + EM = 18 cm
⇒ ED + DK + EF + FM = 18 cm
⇒ ED + DH + EF + HF = 18 cm (∵DK = DH and FM = FH)
⇒ ED + DF + EF = 18 cm.
Hence, the perimeter of △EDF = 18 cm.
15) In the given figure, QR is a common tangent to the given circle, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm then the length of QR is ?
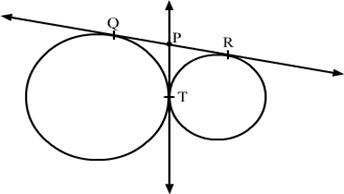
Solution.
We know that tangent segments to a circle from the same external point are congruent.
Therefore, we have
PT = PQ = 3.8 cm and PT = PR = 3.8 cm
∴ QR = QP + PR = 3.8 + 3.8 = 7.6 cm.
Hence, the length of QR is 7.6 cm.
16) In the given figure, O is the centre of the circle AB is a chord and AT is the tangent at A. If ∠AOB = 100∘ then ∠BAT is equal to ?
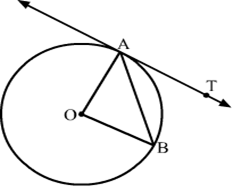
Solution.
Given: AO and BO are the radius of the circle
Since, AO = BO
∴ △AOB is an isosceles triangle.
Now, in △AOB
∠AOB + ∠OBA + ∠OAB = 180∘ (Angle sum property of triangle)
⇒ 100∘ + ∠OAB + ∠OAB = 180∘ (∠OBA = ∠OAB)
⇒ 2∠OAB = 80∘
⇒ ∠OAB = 40∘
We know that the radius and tangent are perpendicular at their point of contact
∵ ∠OAT = 90∘
⇒ ∠OAB + ∠BAT = 90∘
⇒ ∠BAT = 90∘ − 40∘ = 50∘
YOU ARE READING: Circles Chapter 10 Extra Questions and Solutions For Class 10 CBSE Mathematics
Then the value of ∠BAT is 50∘ .
17) In the given figure, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC = 4 cm then find the length of AP ?
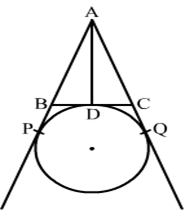
Solution.
We know that tangent segments to a circle from the same external point are congruent.
Therefore, we have
AP = AQ
BP = BD
CQ = CD
Now, AB + BC + AC = 5 + 4 + 6 = 15
⇒AB + BD + DC + AC = 15 cm
⇒AB + BP + CQ + AC = 15 cm
⇒AP + AQ= 15 cm
⇒2AP = 15 cm
⇒AP = 7.5 cm.
Then the length of AP is 7.5 cm.
18) In the given figure, PA and PB are two tangents from an external point P to a circle with centre O. If ∠PBA = 65∘ , find ∠OABand ∠APB?
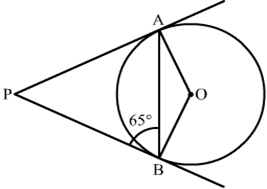
Solution.
We know that tangents drawn from the external point are congruent.
∴ PA = PB
Now, In isoceles triangle APB
∠APB + ∠PBA + ∠PAB = 180∘ [Angle sum property of a triangle]
⇒ ∠APB + 65∘ + 65∘ = 180∘ [∵∠PBA = ∠PAB = 65∘ ]
⇒ ∠APB = 50∘
We know that the radius and tangent are perperpendular at their point of contact
∴∠OBP = ∠OAP = 90∘
Now, In quadrilateral AOBP
∠AOB + ∠OBP + ∠APB + ∠OAP = 360∘ [Angle sum property of a quadrilateral]
⇒ ∠AOB + 90∘ + 50∘ + 90∘ = 360∘
⇒ 230∘ + ∠BOC = 360∘
⇒ ∠AOB = 130∘
Now, In isoceles triangle AOB
∠AOB + ∠OAB + ∠OBA = 180∘ [Angle sum property of a triangle]
⇒ 130∘ + 2∠OAB = 1800 [∵∠OAB = ∠OBA ]
⇒ ∠OAB = 25∘
19) In the given figure, DE and DF are two tangents drawn from an external point D to a circle with centre A. If DE = 5 cm. and DE ⊥ DF then find the radius of the circle ?
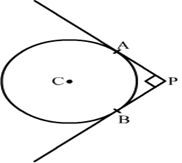
Solution.
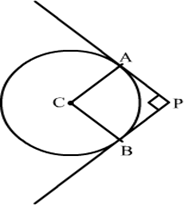
Construction: Join AF and AE.
We know that the radius and tangent are perpendicular at their point of contact
∵∠AED = ∠AFD = 90∘
Since, in quadrilateral AEDF all the angles are right angles
∴ AEDF is a rectangle
Now, we know that the pair of opposite sides are equal in rectangle
∴ AF = DE = 5 cm
Therefore, the radius of the circle is 5 cm.
20) In the given figure, PQ is a tangent to a circle with centre O. A is the point of contact. If ∠PAB = 67∘, then find the measure of ∠AQB ?
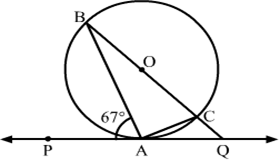
Solution.
We know that a chord passing through the centre is the diameter of the circle.
∵∠BAC = 90∘ (Angle in a semi circle is 90∘)
By using alternate segment theorem
We have ∠PAB = ∠ACB = 67∘
Now, In △ABC
∠ABC + ∠ACB + ∠BAC = 180∘ [Angle sum property of a triangle]
⇒ ∠ABC + 67∘ + 90∘ = 180∘
⇒ ∠ABC= 23∘
Now, ∠BAQ = 180∘ − ∠PAB [Linear pair angles]
= 180∘ − 67∘
= 113∘
Now, In △ABQ
∠ABQ + ∠AQB + ∠BAQ = 180∘ [Angle sum property of a triangle]
⇒ 23∘ + ∠AQB + 113∘ = 180∘
⇒ ∠AQB = 44∘
Then the value of ∠AQB is 44∘