You are going to go through Coordinate Geometry Chapter 7 Extra Questions and Solutions For Class 10 CBSE Mathematics. This post presents to the students a clear conception of how to move with the basics of Extra Questions and answers. The expert prepared The Extra Questions and And Answers. https://cbsencertanswers.com/is very much to make things way simpler and easier for the students. Especially those who are appearing for the board exams. We took every care to make sure that the effort serves the purpose. So, let us find out Coordinate Geometry Chapter 7 Extra Questions and Solutions For Class 10 CBSE Mathematics. On this page, you can find Coordinate Geometry Chapter 7 Extra Questions and Solutions For Class 10 CBSE Mathematics.

1) On which axis do the following points lie?
(i) P (5, 0)
(ii) Q (0, -2)
(iii) R (-4, 0)
(iv) S (0, 5)
Solution.
(i) P (5, 0) lies on x – axis.
(ii) Q (0, -2) lies on y – axis (negation half).
(iii) R (-4, 0) lies on x – axis (negative half).
(iv) S (0, 5) lies on y – axis.
2) Find the distance between the following pair of points (- 6, 7) and (-1, -5) ?
Solution.
Let the given points be P (- 6, 7) and Q (- 1, – 5) . Here, x1 = – 6, y1 = 7 and x2 = -1, y2 = – 5 .
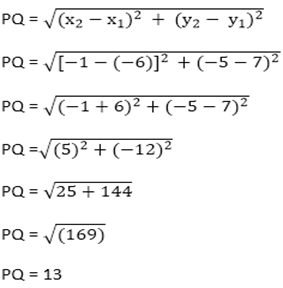
YOU ARE READING: Coordinate Geometry Chapter 7 Extra Questions and Solutions For Class 10 CBSE Mathematics
So, the distance PQ is 13 which connects point P and Q.
3) If the points (2, 1) and (1, -2) are equidistant from the point (x, y), show that x + 3y = 0?
Solution.
Let the given points be P(2, 1) and Q(1,- 2) and R(x, y) . Also, PR = QR (given).
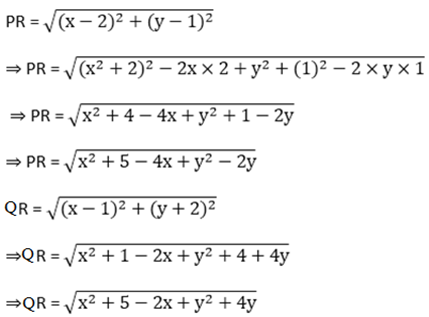
Now we know, PR = QR .Then,
⇒ x2 + 5 – 4x + y2 –2y = x2 + 5 – 2x + y2 + 4y
⇒ x2 + 5 – 4x + y2 – 2y = x2 + 5 – 2x + y2 + 4y
⇒ – 4x + 2x – 2y – 4y = 0
⇒ – 2x – 6y = 0
⇒ – 2(x + 3y) = 0
⇒ -2(x + 3y) = 0
⇒ x + 3y = 0/-2
⇒ x + 3y = 0 Hence Proved.
4) The length of a line segment is of 10 units and the coordinates of one end-point are (2, -3). If the abscissa of the other end is 10, find the ordinate of the other end?
Solution.
It is given that, Length of the line segment is 10 units and Coordinates of one end-point are (2, -3) and the abscissa of the other end is 10. So, let the ordinate of the other end be k.
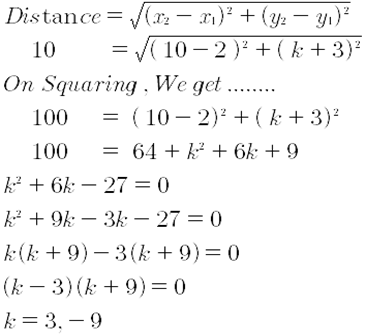
YOU ARE READING: Coordinate Geometry Chapter 7 Extra Questions and Solutions For Class 10 CBSE Mathematics
Therefore, the ordinates of the other end can be 3 or -9.
5) Show that the points A (1,- 2), B (3, 6), C (5, 10) and D (3, 2) are the vertices of a parallelogram?
Solution.
Given that Points A (1,- 2), B (3, 6), C (5, 10) and D (3, 2). It is required to prove that the points are the vertices points of a parallelogram. Vertices of a parallelogram ABCD are: A (1, -2), B (3, 6), C (5, 10) and D (3, 2). We know that,
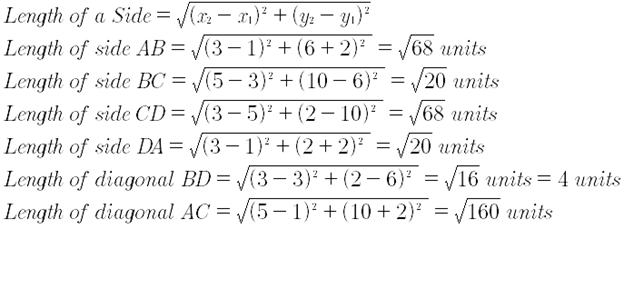
It’s observed that the opposite sides of the quadrilateral formed by the given four points are equal i.e. (AB = CD) & (DA = BC) and also, the diagonals BD & AC are found unequal. Hence Proved.
6) Prove that the points (2a, 4a), (2a, 6a) and (2a + √3a, 5a) are the vertices of an equilateral triangle?
Solution.
Let we consider the vertices of a triangle ABC as A(2 a, 4 a), B(2 a, 6 a) and C(2a + √3a, 5a).
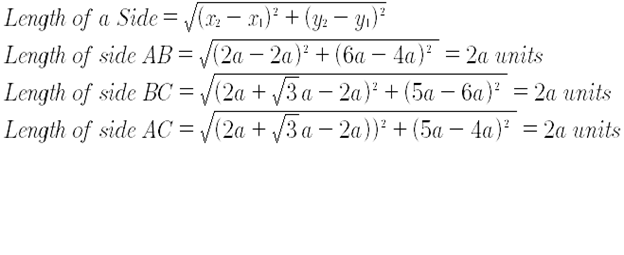
YOU ARE READING: Coordinate Geometry Chapter 7 Extra Questions and Solutions For Class 10 CBSE Mathematics
As all the sides are equal the triangle is an equilateral triangle. Thus, the given vertices are of an equilateral triangle.
7) Show that the quadrilateral whose vertices are (2, -1), (3, 4), (-2, 3) and (-3, -2) is a rhombus.
Solution.
Let A(2, -1), B(3 ,4), C(-2, 3) and D(-3, -2)
Then we have,
Length of AB = √[(3 – 2)2 + (4 – (-1))2] = √[(1)2 + (5)2] = √[1 + 25] = √26 units
Length of BC = √[(3 – (-2))2 + (4 – 3)2] = √[(5)2 + (1)2] = √[25 + 1] = √26 units
Length of CD = √[(-2 – (-3))2 + (3 – 2)2] = √[(-5)2 + (1)2] = √[25 + 1] = √26 units
Length of AD = √[(-3 – 2)2 + (-2 – (-1))2] = √[(-5)2 + (-1)2] = √[25 + 1] = √26 units
As , AB = BC = CD = AD. We can say that, Quadrilateral ABCD is a rhombus.
8) Which point on the y-axis is equidistant from (2, 3) and (-4, 1)?
Solution.
Let A (2, 3) and B (-4, 1) be the given points. Let the point on y – axis equidistant from the above points be C (0, y). Now, we have
AC = √[(0 – 2)2 + (y – 3)2] = √[y2 – 6y + 9 + 4] = √[y2 – 6y + 13]
And,
BC = √[(0 – (-4))2 + (y – 1)2] = √y2 – 2y + 1 + 16] = √[y2 – 2y + 17]
As , AC = BC (given in the condition)
So, AC2 = BC2
y2 – 6y + 13 = y2 – 2y + 17
-4y = 4
y = -1
YOU ARE READING: Coordinate Geometry Chapter 7 Extra Questions and Solutions For Class 10 CBSE Mathematics
Therefore, the point on the y-axis is (0, -1).
9) Find the value of k, if the point P(0, 2) is equidistant from (3, k) and (k, 5)?
Solution.
Let the point P (0, 2) is equidistant from A (3, k) and B (k, 5).
So, PA = PB
PA2 = PB2
(3 -0)2 + (k -2)2 = (k – 0)2 + (5 – 2)2
9 + k2 + 4 – 4k – k2 – 9 = 0
4 – 4k = 0
-4k = -4
Therefore, the value of k = 1
10) Find a point on the x-axis which is equidistant from the points (7, 6) and (-3, 4)?
Solution.
Let A(7, 6) and B(-3, 4) be the given points.
So, PA2 = PB2
(x – 7)2 + (0 – 6)2 = (x + 3)2 + (0 – 4)2
x2 + 49 – 14x + 36 = x2 + 9 + 6x + 16
-20x = -60
x = 3
YOU ARE READING: Coordinate Geometry Chapter 7 Extra Questions and Solutions For Class 10 CBSE Mathematics
Therefore, the point on x-axis is (3, 0).
11) Prove that the points (-2, 5), (0, 1) and (2, -3) are collinear.
Solution.
Let A (-2, 5), B(0, 1) and C (2, -3) be the given points.
So, we have
Length of AB = √[(0 – (-2))2 + (1 – 5)2] = √[(2)2 + (-4)2] = √[4 + 16] = √20 = 2√5 units
Length of BC = √[(2 – 0)2 + (-3 – 1)2] = √[(2)2 + (-4)2] = √[4 + 16] = √20 = 2√5 units
Length of AC = √[(2 – (-2))2 + (-3 – 5)2] = √[(4)2 + (-8)2] = √[16 + 64] = √80 = 4√5 units
Now, it is noticed that,
AB + BC = AC
2√5 + 2√5 = 4√5
4√5 = 4√5
Therefore, we can conclude that the given points (-2, 5), (0, 1) and (2, -3) are collinear.
12) Find a point which is equidistant from the points A (-5, 4) and B (-1, 6). How many such points are there?
Solution.
Let P(x, y) be the equidistant point from points A (-5, 4) and B (-1, 6).
So, the mid-point might be the required point
(x, y) = ( (-5 – 1/ 2), (4 + 6)/2 ) = (-6/2 , 10/2) = (-3, 5)
Thus, the required point is (-3, 5).
Now,
We also know that, AP = BP
So, AP2 = BP2
(x + 5)2 + (y – 4)2 = (x + 1)2 + (y – 6)2
x2 + 25 + 10 + y2 – 8y + 16 = x2 + 2x + 1 + y2 – 12y + 36
10x + 41 – 8y = 2x + 37 – 12y
8x + 4y + 4 = 0
2x + y + 1 = 0
YOU ARE READING: Coordinate Geometry Chapter 7 Extra Questions and Solutions For Class 10 CBSE Mathematics
Therefore, all the points which lie on the line 2x + y + 1 = 0 are equidistant from A and B.
13) Find the coordinates of the point which divides the line segment joining (-1, 3) and (4, – 7) internally in the ratio 3: 4?
Solution.
Let P(x, y) be the required point. By section formula, we know that the coordinates are.
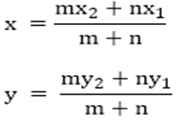
Here, x1 = – 1 y1 = 3 and x2 = 4 y2 = -7 , m: n = 3: 4
Then,
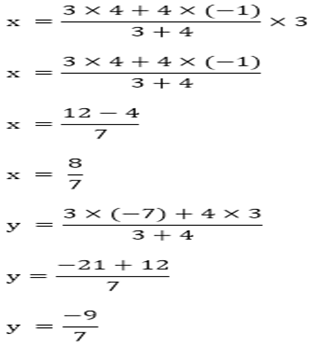
Therefore, the coordinates of P are (8/7, – 9/7).
14) Find the points of trisection of the line segment joining the points (2, – 2) and (-7, 4) ?
Solution.
Let P and Q be the points of trisection of AB such that AP = PQ = OQ.
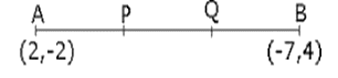
As, P divides AB internally in the ratio 1:2. So, the coordinates of P, by applying the section formula, are given by
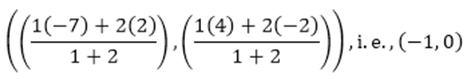
Now. Q also divides AB internally in the ration 2: 1. And the coordinates of Q are given by :
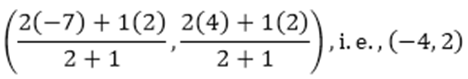
YOU ARE READING: Coordinate Geometry Chapter 7 Extra Questions and Solutions For Class 10 CBSE Mathematics
15) If (a, b) is the mid-point of the line segment joining the points A (10, -6), B(k, 4) and a – 2b = 18, find the value of k and the distance AB?
Solution.
As (a, b) is the mid-point of the line segment A(10, -6) and B(k, 4).
So,
(a, b) = (10 + k / 2, -6 + 4/ 2)
a = (10 + k)/ 2 and b = -1
2a = 10 + k
k = 2a – 10
Given, a – 2b = 18
Using b = -1 in the above relation we get,
a – 2(-1) = 18
a = 18 – 2 = 16
So,
k = 2(16) – 10 = 32 – 10 = 22
Thus,
AB = √[(22 – 10)2 + (4 + 6)2] = √[(12)2 + (10)2] = √[144 + 100] = 2√61 units
Therefore , the value of k is 22 and value of length AB is 2√61 units.
16) Find the ratio in which the point P(x, 2) divides the line segment joining the points A (12, 5) and B (4, -3). Also, find the value of x?
Solution.
Let P divide the line joining A and B and let it divide the segment in the ratio k: 1. Now, using the section formula for the y – coordinate we have
2 = (-3k + 5)/ (k + 1)
2(k + 1) = -3k + 5
2k + 2 = -3k + 5
5k = 3
k = 3/5
Thus, P divides the line segment AB in the ratio of 3: 5
Using value of k, we get the x – coordinate as:
x = 12 + 60/ 8 = 72/8 = 9
YOU ARE READING: Coordinate Geometry Chapter 7 Extra Questions and Solutions For Class 10 CBSE Mathematics
Therefore, the coordinates of point P is (9, 2).
17) Find the coordinates of a point A, where AB is the diameter of circle whose center is (2, -3) and B is (1, 4)?
Solution.
Let the coordinates of point A be (x, y). If AB is the diameter, then the center in the mid-point of the diameter
So,
(2, -3) = (x + 1/ 2, y + 4/ 2)
2 = x + 1/2 and -3 = y + 4/ 2
4 = x + 1 and -6 = y + 4
x = 3 and y = -10
Therefore, the coordinates of A are (3, -10).
18) Find the centroid of the triangle whose vertices are (-2, 3), (2, -1) and (4, 0) ?
Solution.
We know that the coordinates of the centroid of a triangle whose vertices are (x1, y1), (x2, y2), (x3, y3)
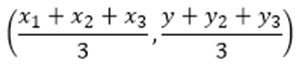
So, the coordinates of the centroid of a triangle whose vertices are (-2, 3), (2, -1) and (4, 0) is:
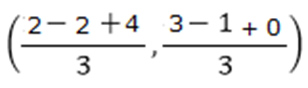
YOU ARE READING: Coordinate Geometry Chapter 7 Extra Questions and Solutions For Class 10 CBSE Mathematics
Thus, centroid of the triangle is (4/3, 2/3).
19) Find the third vertex of a triangle, if two of its vertices are at (-3, 1) and (0, -2) and the centroid is at the origin?
Solution.
Let the coordinates of the third vertex be (x, y). Then, we know that the coordinates of centroid of the triangle are:
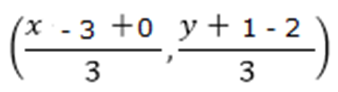
Given that the centroid for the triangle is at the origin (0, 0)
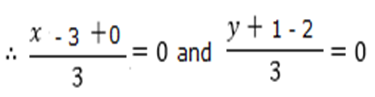
⇒ x – 3 = 0 ⇒ y – 1 = 0
⇒ x = 3 ⇒ y = 1
Therefore, the coordinates of the third vertex is (3, 1).
20) Show that the following sets of points are collinear (2, 5), (4, 6) and (8, 8)?
Solution.
Condition for 3 points to be collinear the area of the triangle formed with the 3 points has to be zero. A(2, 5), B(4, 6) and C(8, 8) be the given points then the area of ΔABC is given by :
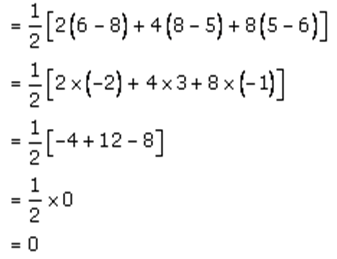
Since, the area (ΔABC) = 0 the given points (2, 5), (4, 6) and (8, 8) are collinear.
YOU ARE READING: Coordinate Geometry Chapter 7 Extra Questions and Solutions For Class 10 CBSE Mathematics
.