
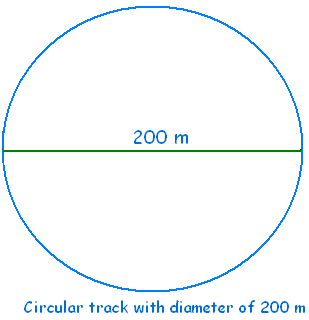
1) An athlete completes one
round of a circular track of diameter 200 m in 40 s. What will be the distance
covered and the displacement at the end of 2 minutes 20 s?
round of a circular track of diameter 200 m in 40 s. What will be the distance
covered and the displacement at the end of 2 minutes 20 s?
ANSWER:-Diameter = 200 m, therefore, radius = 200m/2 =100m
Time of one rotation = 40s
Time after 2m20s = 2 x 60s + 20s = 140s
Distance after 140 s =?
Displacement after 140s =?

(a) Distance after 140s
We know that, distance=velocity ×time
⇒ Distance=15.7m/s ×140 s =
2198 m
2198 m
(b) Displacement after 2 m 20 s i.e. in 140 s
Since, rotating in 40 s=1
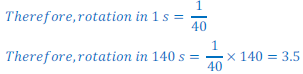
Distance covered in 2 m 20 s = 2198 m
And, displacement after 2 m 20 s = 200m
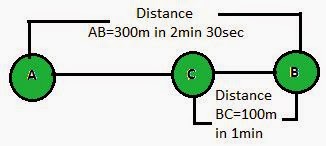
2) Joseph jogs from one end A
to the other end B of a straight 300 m road in 2 minutes 30 seconds and then
turns around and jogs 100 m back to point C in another 1 minute. What are Joseph’saverage
speeds and velocities in jogging (a) from A to B and (b) from A to C?
to the other end B of a straight 300 m road in 2 minutes 30 seconds and then
turns around and jogs 100 m back to point C in another 1 minute. What are Joseph’saverage
speeds and velocities in jogging (a) from A to B and (b) from A to C?
ANSWER:-Total Distance covered from AB =
300 m
300 m
Total time taken = 2 x 60 + 30s =150 s
Therefore, Average Speed from
AB = Total Distance / Total
Time =300 / 150 m s -1 =2 m s -1
Therefore, Velocity from AB
=Displacement AB / Time = 300
/ 150 m s -1 =2 m s -1
/ 150 m s -1 =2 m s -1
Total Distance covered from AC
=AB + BC =300 + 200 m
=AB + BC =300 + 200 m
Total time taken from A to C = Time
taken for AB + Time taken for BC = (2 x 60+30) +60 s = 210 s
taken for AB + Time taken for BC = (2 x 60+30) +60 s = 210 s
Therefore, Average Speed from AC =
Total Distance /Total Time
Total Distance /Total Time
= 400 /210 m s -1
= 1.904 m s -1
Displacement (S) from A to C
= AB – BC
= 300-100 m
= 200 m
Time (t) taken for displacement
from AC = 210 s
from AC = 210 s
Therefore, Velocity from AC = Displacement
(s) / Time(t)
(s) / Time(t)
= 200 / 210 m s -1
= 0.952 m s -1
3) Abdul, while driving to
school, computes the average speed for his trip to be 20 km h−1. On his return trip along
the same route, there is less traffic and the average speed is 40 km h−1. What is the average speed
for Abdul’s trip?
school, computes the average speed for his trip to be 20 km h−1. On his return trip along
the same route, there is less traffic and the average speed is 40 km h−1. What is the average speed
for Abdul’s trip?
ANSWER:-The distance Abdul commutes while
driving from Home to School = S
driving from Home to School = S
Let us assume time taken by Abdul to commutes this distance = t 1
Distance Abdul commutes while driving from
School to Home = S
School to Home = S
Let us assume time taken by Abdul to commutes this distance = t 2
Average speed from home to school v 1av = 20 km
h-1
h-1
Average speed from school to home v 2av = 30 km h-1
Also we know Time taken from Home to School t 1 =S / v 1av
Similarly Time taken form School to Home t 2 =S/v 2av
Total distance from home to school and backward = 2 S
Total time taken from home to school and backward (T) = S/20+
S/30
S/30
Therefore, Average speed (V av) for covering total distance (2S) = Total
Distance/Total Time
Distance/Total Time
= 2S / (S/20 +S/30)
= 2S / [(30S+20S)/600]
= 1200S / 50S
= 24 kmh -1
4) A motorboat starting from
rest on a lake accelerates in a straight line at a constant rate of 3.0 m s −2 for 8.0 s. How far the boat
travels during this time?
rest on a lake accelerates in a straight line at a constant rate of 3.0 m s −2 for 8.0 s. How far the boat
travels during this time?
ANSWER:-Given Initial velocity of motorboat,
u = 0
u = 0
Acceleration of motorboat, a = 3.0
m s -2
m s -2
Time under consideration, t =8.0 s
We know that Distance, s = ut+ (1/2) at 2
Therefore, The distance travel by motorboat = 0
x 8 + (1/2)3.0 x 8 2
x 8 + (1/2)3.0 x 8 2
= (1/2) x 3 x 8 x 8 m
= 96 m
5) A driver of a car
travelling at 52 km h−1 applies the brakes and accelerates uniformly in the opposite
direction. The car stops in 5 s. Another driver going at 3 km h−1 in another car applies his brakes
slowly and stops in 10 s. On the same graph paper, plot the speed versus time
graphs for the two cars. Which of the two cars travelled farther after the
brakes were applied?
travelling at 52 km h−1 applies the brakes and accelerates uniformly in the opposite
direction. The car stops in 5 s. Another driver going at 3 km h−1 in another car applies his brakes
slowly and stops in 10 s. On the same graph paper, plot the speed versus time
graphs for the two cars. Which of the two cars travelled farther after the
brakes were applied?
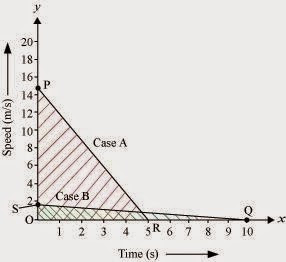
ANSWER:–
Distance Travelled by first car before coming to rest =Area of
△ OPR
= (1/2) x OR x OP
= (1/2) x 5 s x 52 kmh-1
= (1/2) x 5 x (52 x 1000) / 3600) m
= (1/2) x 5x (130 / 9) m
= 325 / 9 m
= 36.11 m
Distance Travelled by second car before coming to rest
=Area of △ OSQ
= (1/2) x OQ x OS
= (1/2) x 10 s x 3 kmh-1
= (1/2) x 10 x (3 x 1000) /
3600) m
= (1/2) x 10 x (5/6) m
= 5 x (5/6) m
= 25/6 m
= 4.16 m
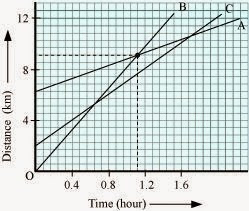
6) Fig 8.11 shows the
distance-time graph of three objects A, B and C. Study the graph and answer the
following
distance-time graph of three objects A, B and C. Study the graph and answer the
following
Questions:
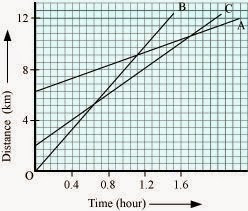
(a) Which of the three is travelling the
fastest?
fastest?
(b) Are all three ever at the same point on the
road?
road?
(c) How far has C travelled when B passes A?
(d)How far has B travelled by the time it passes
C?
C?
ANSWER 🙁 a) Object B
(b) No
(c) 5.714 km
(d) 5.143 km

Speed = slope of the graph
Since slope of object B is greater than objects A and C, it is
travelling the fastest.
travelling the fastest.
(b) All three objects A, B and C never meet at a single point.
Thus, they were never at the same point on road.
Thus, they were never at the same point on road.
7) A ball is gently dropped
from a height of 20 m. If its velocity increases uniformly at the rate of 10 m
s −2, with what velocity will it strike the ground? After what time
will it strike the ground?
from a height of 20 m. If its velocity increases uniformly at the rate of 10 m
s −2, with what velocity will it strike the ground? After what time
will it strike the ground?
ANSWER:-Let us assume, the final velocity
with which ball will strike the ground be ‘v’ and time it takes to strike the
ground be’t’
with which ball will strike the ground be ‘v’ and time it takes to strike the
ground be’t’
Initial Velocity of ball, u =0
Distance or height of fall, s =20 m
Downward acceleration, a =10m s -2
As we know, 2as =v 2-u2
v 2 = 2as+ u2
= 2 x 10 x 20 + 0
= 400
∴ Final velocity of
ball, v = 20ms-1
ball, v = 20ms-1
t = (v-u)/a
∴Time taken by the
ball to
strike = (20-0)/10
ball to
strike = (20-0)/10
= 20/10
= 2 seconds
8) The speed-time graph for a car is shown is Fig. 8.12.
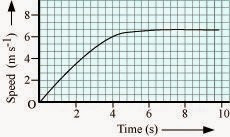
(a) Find out how far the car travels in the first 4 seconds. Shade
the area on the graph that represents the distance travelled by the car during
the period.
the area on the graph that represents the distance travelled by the car during
the period.
(b) Which part of the graph represents
uniform motion of the car?
uniform motion of the car?
a)
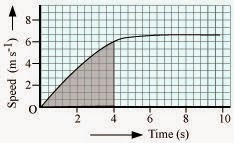
ANSWER:–
The shaded area which is equal to 1 / 2 x 4 x 6 = 12 m represents
the distance travelled by the car in the first 4 s.
the distance travelled by the car in the first 4 s.
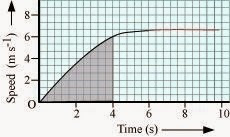
b) The part of the graph between time 6 s to 10 s represents uniform motion of the car.
10) State which of the
following situations are possible and give an example for each of these:
following situations are possible and give an example for each of these:
(a) An object with a constant
acceleration but with zero velocity.
acceleration but with zero velocity.
(b) An object moving in a
certain direction with acceleration in the perpendicular direction.
certain direction with acceleration in the perpendicular direction.
ANSWER :-(a) Possible When a ball is
thrown up at maximum height, it has zero velocity, although it will have
constant acceleration due to gravity, which is equal to 9.8 m/s2.
thrown up at maximum height, it has zero velocity, although it will have
constant acceleration due to gravity, which is equal to 9.8 m/s2.
(b) Possible When a car is moving
in a circular track, its acceleration is perpendicular to its direction.
in a circular track, its acceleration is perpendicular to its direction.
10) An artificial satellite
is moving in a circular orbit of radius 42250 km. Calculate its speed if it
takes 24 hours to revolve around the earth
is moving in a circular orbit of radius 42250 km. Calculate its speed if it
takes 24 hours to revolve around the earth
ANSWER:-Radius of the circular orbit, r=
42250 km
42250 km
Time taken to revolve around the earth, t= 24 h
Speed of a circular moving object, v= (2π r)/t
= [2× (22/7) ×42250 × 1000] / (24 × 60 × 60)
= (2×22×42250×1000) / (7 ×24× 60 × 60) m s -1
=3073.74 m s -1